Степень многочлена - это наибольшая степень входящего в него одгночлена.
Степень одночлена - это сумма степеней всех переменных, входящих в его состав.
а) многочлен 3х⁵ + 2х³ + 4 состоит из следующих членов: 3х⁵; 2х³ и 4, его степень - 5;
б) многочлен 2х⁴ - 3х + 2 состоит из следующих членов: 2х4; -3х и 2, его степень - 4;
в) многочлен х⁵ + х⁴ - 2х² - 1 состоит из следующих членов: х⁵; х⁴; -2х² и -1, его степень - 5;
г) многочлен 2m⁶ + 7 состоит из следующих членов: 2m⁶ и 7, его степень - 6;
д) многочлен 4ху⁶ + ху² - х² + у⁸ состоит из следующих членов: 4ху⁶; ху²; -х² и у⁸, его степень - 8;
е) многочлен а³ - bc - 7 состоит из следующих членов: a³; -bc и -7, его степень - 3.
1 (-бесконечность;+бесконечность) 2 (- бесконечность;-7\4)U(-7\4;+бесконечность) 3 [-7;+бесконечность) 4 (-бесконечность;1/2) 5(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность) 6(-бесконечность;+бесконечность)
Пошаговое объяснение:
Область определения это такие числа, которые может принимать переменная x.
1.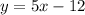 (здесь при любых числах выражение решается,т.е. нет ограничений => (-бесконечность;+бесконечность)
(здесь при любых числах выражение решается,т.е. нет ограничений => (-бесконечность;+бесконечность)
2.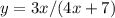 (В данном случае, ограничение присутствует, знаменатель дроби не должен быть равен нулю. (старое правило-на 0 делить нельзя)
(В данном случае, ограничение присутствует, знаменатель дроби не должен быть равен нулю. (старое правило-на 0 делить нельзя)
3.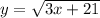 (Под корнем всегда должно быть неотрицательное число)
(Под корнем всегда должно быть неотрицательное число)
4.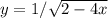 (знаменатель не должен быть равен 0, а так же не должен быть отрицательным)
(знаменатель не должен быть равен 0, а так же не должен быть отрицательным)
5.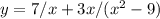 (знаменатель не должен быть равен 0)
(знаменатель не должен быть равен 0)
6.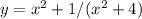 (знаменатель не должен быть равен 0, но если решить, можно понять что знаменатель положителен при любых x)
(знаменатель не должен быть равен 0, но если решить, можно понять что знаменатель положителен при любых x)
(-бесконечность;+бесконечность)