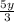

 (разделим обе части на у)
(разделим обе части на у)ответ:
y=x+2 разрыв в точках (-5,-3) и (2,4)
пошаговое объяснение:
числитель
знаменатель по теореме виета корни многочлена: x1=-5; x2=2
отсюда получается наша дробь равна:
с разрывом в точках x=2, x=-5,
т.е. строим прямую y=x+2, которая пересекает ось oy в точке (0,2) и ось ox в точке (-2,0) и с разрывам в точках (-5,-3) и (2,4)

Пример 2Метод: приведение под знак дифференциала.Но так как степень n = 4 чётная, то отрицательного значения в аргументе логарифма быть не может, максимальное значение: ln|1 + 0| = ln|1| = 0, следовательно, модуль можно убрать.
Пример 3Метод: по частям.Так как в подинтегральном выражении модуль, нужно рассматривать два случая:
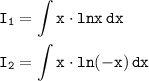
Рассмотрим первый интеграл: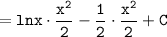
Второй интеграл отличается от первого знаком минус в аргументе, поэтому ответ будет таким же, различаться будут лишь аргументы (это исключительный случай)Так как это кусочно-заданная функция
, нам необходимо написать условия для отдельных формул. Так, для I₁ условие x ≥ 0, а для I₂ < 0.