Угол ACB равен 54 градусам. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138 градусам. Найдите угол DAE. ответ дайте в градусах.
----------
Скорее всего, эта задача дается с готовым рисунком.
Угол АСВ образован секущими ВС и АС. пересекающим окружность с центром О в точках D и E
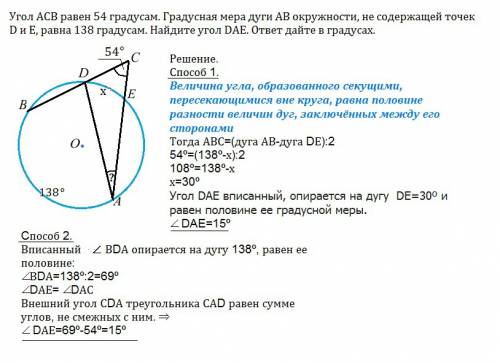
Решение.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Тогда АВС=(дуга АВ-дуга DЕ):2
54º=(138º-х):2
108º=138º-х
х=30º
Угол DAE вписанный, опирается на дугу DЕ=30º и равен половине ее градусной меры.
∠ DAE=15º
Cпособ 2.
Вписанный угол ВDА опирается на дугу 138º, равен ее половине:
∠ВDА=138º:2=69º
∠DАЕ= ∠DАС
Внешний угол СDА треугольника САD равен сумме углов, не смежных с ним. ⇒
∠ DАЕ=69º-54º=15º
х км – расстояние от дома до остановки
у км - расстояние от остановки до школы
54 мин = 54/60 часа
56 мин = 56/60 часа
Имеем два уравнения, которые образуют систему:
{х/6 + у/30 = 54/60
{х/5 + у/36 = 56/60
Преобразуем:
{10х/60 + 2у/60 = 54/60
{36х/180 + 5у/180 = 168/180
получим:
{10х + 2у = 54 это уравнение умножим на (- 5)
{36х + 5у = 168 это умножим на 2
имеем:
{- 50х - 10у = - 270
{72х + 10у = 336
Сложим эти уравнения:
- 50х - 10у + 72х + 50х = – 270 + 336
72х - 50х = 66
22х = 66
х = 66 : 22
х = 3 км - искомое расстояние от дома до остановки
ответ: 3 км
Пошаговое объяснение:
из ΔАВД, где ∠А=90°,∠Д=30°⇒∠В=90-30=60°
А если ВТ - биссектриса, то ∠СВТ=∠ТВД=30°, тогда
из ΔДТВ , где∠Д=30° и ∠В=30°⇒ΔДТВ - равнобедренный, ВТ=ТД=8см
Из ΔАВТ, где∠А=90°,∠В=30°⇒ что катет АТ лежит против угла 30°⇒
АТ=ТВ:2=8:2=4⇒
АД=АТ+ТД=4+8=12см