Задание 3.
При каком значении переменной значение выражения 5x − 0,4(7x − 9) равно 2,94?

👇

Увидеть ответ

Ответ:

01061969

11.02.2021

Записываем в виде уравнения и решаем:

5x - 0,4(7x - 9) = 2,94

5x - 2,8x + 3,6 = 2,94

2,2x = 2,94 - 3,6

2,2x = -0,66

x = -0,66 ÷ 2,2

x = -0,3

ОТВЕТ: при -0,3

4,6(54 оценок)

Открыть все ответы

Ответ:

Matvei200322

11.02.2021

Объект труда: ручка для молотка.
Ход урока
I. Организационно-подготовительная часть

Приветствие учителя, контроль посещаемости.

Проверка готовности учащихся к уроку

II. Теоретическая часть

Повторение пройденного материала.

Карточка № 1

Прочитать вопрос и ответить на него

Что такое шиповое ступенчатое соединение?

Для этого вспомни:

Какие существуют виды ступенчатого соединения;

Как правильно разметить и выполнить соединение;

Что применяется для сборки соединения;

Где применяется ступенчатое соединение;

Сделай вывод.

Примерные ответы учащихся.

Изготовлений многих деталей из древесины бруски соединяют между собой. Самым простым является соединение в половину бруска (вполдерева), ступенчатое. Бруски соединяются врезанными на половину участками.

Соединение может быть по длине, под прямым или другим углом.

Первым этапом является разметка, сначала размечают базовую линию длинны заготовки. Далее размечают, толщину вырезаемых участков, применяя для этого рейсмус. После этого размечают длину вырезаемых участков. После разметки приступают к пилению. Сначала делают пропил вдоль волокон, а потом пропил поперек волокон, для удаления части заготовки.

Выполняется соединение, нужно стремится к тому, чтобы детали прямо из после пилы, без дополнительной подгонки плотно прилегали друг к другу. Но иногда все, же приходится исправлять погрешности в работе при стамески и напильника.

Для того чтобы зафиксировать соединение, можно воспользоваться гвоздями, шурупами или клеем. Более надежным получается соединение на нагеле. Нагель- это деревянный цилиндрический стержень диаметром 6-10 мм. Нагель устанавливается на клей в просверленное через соединение отверстие. Выступающие концы нагеля срезают и выравнивают наждачной бумагой. Соединение упрочнятся при применении двух нагелей.

Ступенчатое соединение нашло очень широкое применение из- за простоты соединения. С такого соединения можно собрать рамки, подставки: для цветов, стендов, плакатов, новогодней елки.

2. Сообщение учащихся.

«Из истории изделий цилиндрической формы». Про колесо

Рис. 1. Деревянное колесоЧто может быть проще колеса?! А, между прочим, на создании этой простой и совершенной конструкции люди потратили не о сотню лет. Раскопки археологов подтверждают факт о том, что наши далёкие предки задолго до цивилизации использовали это примитивное, но с большими практическими возможностями техническое сооружение (рис. 1).Попробуйте вспомнить сегодня машину, в которой не было ни одного колеса. Чем же оно замечательно?Если взять, например, ствол толстого дерева, распилить его поперек несколько раз, то получим много деревянных диск кругляшек.Почему же мы говорим, что кругляшка не колесо?Потому что у колеса есть секрет, которого нет у кругляшек и отверстие посередине. Этот пустяк превращает обыкновенную и кругляшку в настоящее колесо: отверстие, о которой говорится, распопе на точно в центре окружности.Это значит, что колесо можно насадить на ось и заставить везти любой груз - в тачке или телеге... Только подумайте, что получилось бы, если бы отверстие находилась не в центре, а где - нибудь сбоку? На таком кособоком колесе далеко не уедешь: оно катится по ровной дороге, а ось то вверх, то вниз поднимается, другое дело, когда ось посередине: центр окружности - замечательное место. От него до любой точки окружности одно и то же состояние - колесо катится, а ось всегда остается на одинаковой высоте от земли.Нет, самое первое колесо было непросто придумать и сделать тактичным. При его к полезному делу тоже было непросто. Как же с использование примитивных ручных инструментов можно было придать колесу совершенную форму?На стенах древних египетских пирамид сохранились надписи изображения, повествующие о том, как делались катки. На их рисунках отчетливо видны люди, которые обтачивают гигантский каменный блок, чтобы придать ему круглую форму, конечно, никто из нас не видел, как это происходило на самом деле. Но историки говорят, что именно так могло быть в действительности.Не сразу человек додумался до обыкновенных катков. Но и катков до колеса путь был не близкий - несколько тысячелетий.Эволюция колеса на этом также не завершилась. Спустя некоторое время наши предки додумались заменить цельное деревянное колесо на колесо с деревянными спицами, что сделало возможным перевозки на дальнее расстояние. Уж в таком-то видемы и сегодня можем видеть великое произведение мысли рук человеческих. Как правило, их делали ручными стругами, дорабатывая созданные природой круглой формы стволы тонких, но твердых пород древесины. Поэтому, если изобретение колеса по первым шагом человека, то появление колеса со спицами можно назвать вторым

4,7(92 оценок)

Ответ:

obuhovasveta

11.02.2021

$\beta\in[0;1]:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{n}}=\alpha$

Тогда, по признаку Коши, при 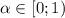$\alpha\in[0;1)$ ряд сходится, при 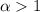$\alpha 1$ расходится.

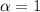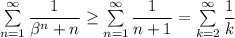При $\alpha=1$ имеем $\sum\limits_{n=1}^\infty\dfrac{1}{\beta^n+n}\geq \sum\limits_{n=1}^\infty\dfrac{1}{n+1}= \sum\limits_{k=2}^\infty\dfrac{1}{k}$ Гармонический ряд расходится, а тогда исходный ряд расходится по признаку сравнения.

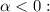
$\alpha$

При 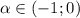$\alpha\in(-1;0)$ ряд сходится, т.к. ряд из модулей (по доказанному выше) сходится.

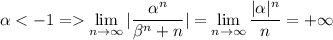$\alpha\lim\limits_{n\to\infty}{|\dfrac{\alpha^n}{\beta^n+n}|}=\lim\limits_{n\to\infty}{\dfrac{|\alpha|^n}{n}}=+\infty$ необходимое условие не выполнено, а значит ряд расходится.

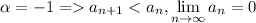$\alpha=-1= a_{n+1}$ , а тогда по признаку Лейбница ряд сходится.

$\beta1:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n}}=\dfrac{\alpha}{\beta}$

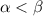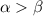Тогда при $\alpha$ ряд сходится, при $\alpha\beta$ расходится.

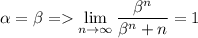$\alpha=\beta=\lim\limits_{n\to\infty}{\dfrac{\beta^n}{\beta^n+n}}=1$ - необходимое условие не выполнено, ряд расходится.

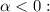
$\alpha$

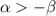Тогда при $\alpha-\beta$ ряд сходится.

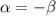При $\alpha=-\beta$ необходимое условие не выполнено, ряд расходится.

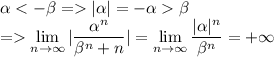$\alpha|\alpha|=-\alpha\beta\\=\lim\limits_{n\to\infty}{|\dfrac{\alpha^n}{\beta^n+n}|}=\lim\limits_{n\to\infty}{\dfrac{|\alpha|^n}{\beta^n}}=+\infty$ необходимое условие не выполнено, ряд расходится.