Перед выходом завел свои часы, и установил, скажем, на 12-00.
Пошел к приятелю, и когда пришел - засек время на часах приятеля.
Уходя от приятеля, тоже засек время на его часах, таким образом, узнав, сколько времени я был у него в гостях.
Придя домой - посмотрел на часы, и узнал, сколько времени я не был дома. Вычитаем из этого времени время, которое я был в гостях, получаем время, затраченное на дорогу туда и обратно.
Делим это время пополам - получаем время на дорогу от приятеля до моего дома. Зная, во сколько я вышел от приятеля, добавляем время затраченное на дорогу, и получаем текущее время.
Ну что же, исходим из условия.
Примем количество мальчиков за
. Тогда весь класс составит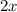 
человек. Тогда отличников в классе всего 
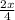(так как 
).
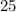Из отличников одна треть - это девочки, а две трети - это мальчики. То есть, девочек в числе отличников всего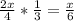
, а мальчиков в числе отличников: 
.
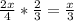Восемь мальчиков отличниками не являются, тогда остальные являются отличниками. Особое внимание на этот вывод - он выводит задачу из относительности в конкретные расчёты.
Такое условие может соблюдаться только при одном равенстве, которое сопоставляет общее количество мальчиков к количеству мальчиков-отличников:
Таким образом, в классе 12 мальчиков, 12 девочек и 24 ученика в классе.
----
Предлагаю проверить задачу по условию.
В классе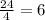
отличников. Треть из них - девочки, значит, в классе 
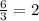отличницы и 
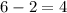отличника. Восемь мальчиков в число отличников не входят: прибавив 8 к 4, получаем общее количество мальчиков в классе: 12.
По смыслу также подходит, решение подтверждено.