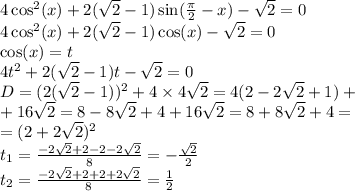
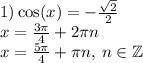
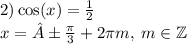
ответ:
симметрия в природе
целью данной работы является определение роли симметрии в живой и неживой природе.
симметрия является одной из наиболее и одной из наиболее общих закономерностей мироздания: живой, неживой природы и общества. принципы симметрии играют важную роль в и , и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.
законы природы, неисчерпаемой в своем многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
существует две группы симметрии. к первой группе относится симметрия положений, форм, структур. это та симметрия, которую можно непосредственно видеть. она может быть названа симметрией. вторая группа характеризует симметрию явлений и законов природы. эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать симметрией.
исследование симметрии земли как планеты в целом позволяет систематически и с соответствующей детальностью проанализировать динамику формирования фигуры земли, т. е. рассмотреть качественную и количественную роль различных силовых полей, воздействие которых определяет эту фигуру.
суммарное воздействие силы земного тяготения можно изобразить в виде пучка бесчисленного множества одинаковых векторов, направленных к одной общей точке – центру земли. симметрия такого пучка, так же как и симметрия идеального и неподвижного шара отвечает бесчисленному множеству осей симметрии бесконечного порядка (осей вращения) и бесчисленному множеству плоскостей симметрии, пересекающихся в одной точке – центре шара. симметрия воздействующего на землю поля солнечной радиации соответствует, очевидно, симметрии конуса, ось которого совпадает с осью солнце – земля. поле солнечной радиации в окрестностях земли – симметрия цилиндра.
круговая симметрия обладает большой общностью. главная особенность кругового преобразования состоит в том, что оно всегда сохраняет углы фигуры и сферу, и всегда переходит в сферу другого радиуса. вот почему кристаллы любого вещества могут иметь самый разный вид, но углы между гранями всегда постоянны. каждая снежинка – это маленький кристалл замерзшей воды. форма снежинок может быть разнообразной, но все они симметрией – поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
на явление симметрии в живой природе обратили внимание еще пифагорейцы в связи с развитием ими учения о гармонии. установлено, что в природе наиболее распространены два вида симметрии - «зеркальная» и «лучевая» (или «радиальная») симметрии.
у цветковых растений в большинстве проявляется радиальная и зеркальная симметрия. цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей. к формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется «ромашко-грибной» симметрией. для листьев характерна зеркальная симметрия.
типы симметрии у животных: центральная; осевая; радиальная; билатеральная (зеркальная); поступательная и поступательно-вращательная; винтовая, а также спиральная симметрия. примером винтовой симметрии может служить раковина улитки (правый винт). зеркальная симметрия хорошо видна у бабочки; симметрия левого и правого проявляется здесь с почти строгостью.
также отметим зеркальную симметрию человеческого тела: правое и левое полушария головного мозга, правые и левые кисти рук, ступни ног и т.д. она же проявляется в гармонии человеческих движений, как в танцах, так и в технической работе, где проявляется закономерность.
принципы симметрии лежат в основе теории относительности, квантовой механики, твердого тела, атомной и ядерной , элементарных частиц. эти принципы наиболее ярко выражаются в свойствах инвариантности законов природы. речь при этом идет не только о законах, но и других, например, биологических. примером биологического закона сохранения может служить закон наследования. молекула днк, являющаяся носителем наследственной информации в живом организме, имеет структуру двойной правой спирали.
принцип «симметрии» широко используется в искусстве. бордюры, используемые в архитектурных и скульптурных произведениях, орнаменты, используемые в прикладном искусстве, - все это примеры использования симметрии.
на основании вышесказанного можно утверждать, симметрия в природе проявляется в самых различных объектах материального мира и отражает наиболее общие, наиболее его свойства. поэтому исследование симметрии разнообразных природных объектов и сопоставление результатов является удобным и надежным инструментом познания основных закономерностей существования материи. без принципа симметрии нельзя рассмотреть ни одной проблемы, будь то проблема жизни или проблема контактов с внеземными цивилизациями.
ответ:
пошаговое объяснение:
всего было n * (n - 1) / 2 игр между профессионалами (в каждой такой игре победил профессионал), 2n * (2n - 1)/2 игр между любителями (соответственно, в таких играх побеждали любители) и n * 2n = 2n^2 игр, в которых приняли участие профессионал и любитель (допустим, в x из них победил профессионал, и в 2n^2 - x победил любитель).
оценим возможное отношение числа побед профессионалов к числу побед любителей, оно равно
[*}
это отношение будет наименьшим при x = 0, когда все любители обыграли всех профессионалов, тогда оно равно (n - 1)/(8n - 2).
это отношение будет наибольшим при x = 2n^2 (это соответствует всем поражениям любителей в матчах с профессионалами), значение отношения (5n - 1)/(4n - 2).
найдем, при каких n 7/5 попадает в этот промежуток:
итак, все возможные n - 1, 2 и 3. заметим, что общее количество игр 3n (3n - 1)/2 должно быть кратно 7 + 5 = 12, это выполнено только для n = 3.
подробнее - на -