15
Пошаговое объяснение:
1)12:4=3
2)12+3=15

1) Если х < 0, то левая часть неотрицательна в силу модуля, правая - отрицательна. Верно всегда, в ответ. 2) Если х = 0, то 30 >= 0 - верно. 3) Если х > 0, то можно возвести обе части в квадрат и представить это в виде разности квадратов:
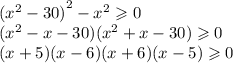
Методом интервалов при х > 0: х принадлежит (0;5] U [6; + беск.)
В итоге получаем ответ: ( - беск. ; 5 ] U [ 6 ; + беск. ). Не являются решением данного неравенства х принадлежит (5;6), но в этот интервал не входят целые числа, поэтому их количество равно 0
ответ: 0.
P(x;y)dx+Q(x;y)dy
является полным дифференциалом, если
∂P/∂y=∂Q/∂x.
∂P/∂y=((x+y)/(xy))`y=((x+y)`y·(xy)–(xy)`y·(x+y))/(xy)2= –x2/(xy)2= – 1/y2
∂Q/∂x=(1/y2)·(y–x)`x=(1/y2)·(–1)=–1/y2
∂P/∂y=∂Q/∂x
Данное уравнение – уравнение в полных дифференциалах
Это значит
∂U/∂x=P(x;y)
∂U/∂y=Q(x;y)
Зная, частные производные можем найти U(x;y)
U(x;y)= ∫ (∂U/∂x)dx= ∫ P(x;y)dx= ∫ (x+y)dx/(xy)=
=(1/y) ∫ (x+y)dx/x=(1/y) ∫ (1+(y/x))dx=(1/y)·x+(1/y)·yln|x|+ φ (y)=
=(x/y)+ln|x|+ φ(y)
Находим
∂U/∂y= ((x/y)+ln|x|+ φ(y))`y=x·(1/y)`+0+ φ `(y)= (–x/y2)+φ `(y)
Так как
∂U/∂y=Q(x;y)
то
(–x/y2)+φ `(y) =(y–x)/y2;
⇒
φ `(y)=1/y
φ(y)=ln|y|+C
U(x;y)=(x/y)+ln|x|+ φ(y)=(x/y)+ln|x|+ln|y|+C
О т в е т.U(x;y)=(x/y)+ln|x·y|+C
15
Пошаговое объяснение:
Первым делается деление, потом сложение