ответ: 3 ученика на 4 ,,15 на 5,, а остальные на 3 и 2
Пошаговое объяснение: если учеников было 30 а 5 было у 50% то 50 процент 30-и это 15 а 4 взяли 20% а 20% 14-и это 2
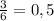 , следовательно вероятность того, что выпадет число, которое не больше 3, тоже равна 0,5, то есть при одном бросании кубика с одной и той же вероятностью реализуется либо событие 1 (выпало число больше 3), либо событие 2 (выпало число не больше 3). Отсюда можно сделать вывод, что при двух бросках может быть 4 события: 1-1, 1-2, 2-1, 2-2. Нам же нужно первое событие. Тогда вероятность того, что выпадет число, больше трех, равна
, следовательно вероятность того, что выпадет число, которое не больше 3, тоже равна 0,5, то есть при одном бросании кубика с одной и той же вероятностью реализуется либо событие 1 (выпало число больше 3), либо событие 2 (выпало число не больше 3). Отсюда можно сделать вывод, что при двух бросках может быть 4 события: 1-1, 1-2, 2-1, 2-2. Нам же нужно первое событие. Тогда вероятность того, что выпадет число, больше трех, равна 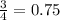

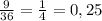
Ученики написавшие на 4- 6 человек.
Ученики написавшие на 5- 15 человек
Пошаговое объяснение:
Находим 20 процентов от 30, что равно 6.
Находим 50 процентов от 30, что равно 15.