В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра: Ad=3,A1A=7,AB=4.Точка О принадлежит ребру BB1 и делит его в отношении 3:4,считая от вершины B.
Найдите площадь сечения этого параллелепипеда плоскостью,проходящей через точки А,О,С1.Результат возведите в квадрат и запишите ответ.
1)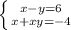
x-y=6
x=6+y 6+у+6у+у^2=-4
у^2+7у+10=0
у1= -2
у2= 5
х1= 6+2= 8
х2= 6-5 = 1
ответ: (8; -2) ; (1;5)
5)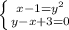
у-х+3=0
-х=-3-у
х= 3-у 3-у-1=y^2
-у^2-у+2=0
y^2+y-2=0
y1= 1
y2= -2
x1= 3-1 = 2
x2= 3+2 = 5
ответ: (2;1) ; (5;-2)
3)
x-y=1
-y=1-x
y= x-1 x^2-2x+2-26=0
x^2-2x-24=0
x1= 6
x2= -4
y1= 6-1 = 5
y2= -4-1 = -1
ответ: (6;5) ; (-4; -1)