1. Выполните действия:
а)
б) 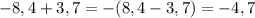
в)
г) 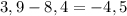
д)
е) 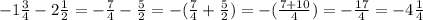
2. Найдите значение выражения:
1) 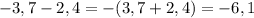
2)
3) 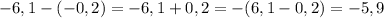
4)
3. Решите уравнение:
а) 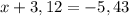
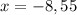
________________________________________________
(это проверка)
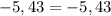
================================================
б)
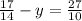
4. Найдите расстояние между точками А(-2,8) и В (3,7) на кооординатной прямой.
Исходя из данных условия задания получается прямоугольный треугольник, катеты которого равны 1 и 5 соответственно
по теореме Пифагора: 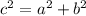
5. Напишите все целые значения n, если 4 меньше|n|меньше 7.
-6; -5; 5; 6
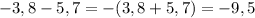
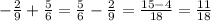
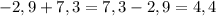
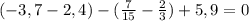
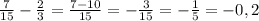
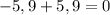
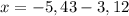
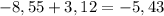
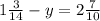
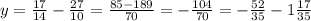
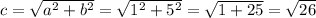
Числитель и знаменатель разложим на множители
\lim_{x \to \inft1} \frac{3 x^{2} -2x+1}{ x^{2} -4x+3} =\lim_{x \to \inft1} \frac{(3x+1)*(x-1)}{(x-3)*(x-1)}=\lim_{x \to \inft1} \frac{3x+1}{x-3} = \frac{4}{-2}=-2lim
x→\inft1
x
2
−4x+3
3x
2
−2x+1
=lim
x→\inft1
(x−3)∗(x−1)
(3x+1)∗(x−1)
=lim
x→\inft1
x−3
3x+1
=
−2
4
=−2
2. Числитель и знаменатель разделим на x²
\lim_{x \to \infty} \frac{3 x^{2} +5x+4}{2 x^{2} -x+1} = \lim_{x \to \infty} \frac{3+ \frac{5}{x}+ \frac{4}{ x^{2} } }{2- \frac{1}{x} + \frac{1}{ x^{2} } } = =\lim_{x \to \infty} \frac{3+ \frac{5}{oo}+ \frac{4}{oo^{2} } }{2- \frac{1}{oo} + \frac{1}{ oo^{2} } } = \frac{3}{2}lim
x→∞
2x
2
−x+1
3x
2
+5x+4
=lim
x→∞
2−
x
1
+
x
2
1
3+
x
5
+
x
2
4
==lim
x→∞
2−
oo
1
+
oo
2
1
3+
oo
5
+
oo
2
4
=
2
3
3. Приводим ко второму замечательному пределу
\lim_{x \to \infty} ( \frac{2x-7}{2x-3}) ^{4x+1}= \lim_{x \to \infty} ( \frac{2x-3 -4}{2x-3}) ^{4x+1}= \lim_{x \to \infty} (1- \frac{4}{2x-3} ) ^{4x+1}lim
x→∞
(
2x−3
2x−7
)
4x+1
=lim
x→∞
(
2x−3
2x−3−4
)
4x+1
=lim
x→∞
(1−
2x−3
4
)
4x+1
Пусть t=- \frac{4}{2x-3}t=−
2x−3
4
, откуда x= \frac{3}{2} - \frac{2}{t}x=
2
3
−
t
2
При этом t→0
Делаем замену
\lim_{t \to \inft0}(1+t)^{7- \frac{8}{t}} =\lim_{t \to \inft0}(1+t) ^{7} *(1+t) ^{- \frac{8}{t}} = =\lim_{t \to \inft0}(1+t) ^{7} *\lim_{t \to \inft0}((1+t)^{\frac{1}{t}} ) ^{-8} =1*( \lim_{t \to \inft0}(1+t)^{\frac{1}{t}} ) ^{-8} =e ^{-8}lim
t→\inft0
(1+t)
7−
t
8
=lim
t→\inft0
(1+t)
7
∗(1+t)
−
t
8
==lim
t→\inft0
(1+t)
7
∗lim
t→\inft0
((1+t)
t
1
)
−8
=1∗(lim
t→\inft0
(1+t)
t
1
)
−8
=e
−8
ответ: - 45/2 = -11 1/2
Пошаговое объяснение:
22*(-45/44) = - 45/2 = -11 1/2