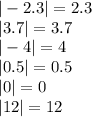
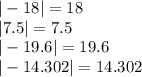
Даны точки точки М(1;7;5), N(-5;4;-7), К(-5; 3; -3).
Находим уравнение через точки точки М и N.
(x-1)/(-6) = (y - 7)/(-3) = (z - 5)/(-12).
Подставим координаты точки К(-5; 3; -3):
(-5 - 1)/(-6) ≠ (3 - 7)(-3) ≠ (-3 - 5)/(-12). Нет, не лежит точка К на прямой MN.
Расстояние между точками равно:
MN NK MK
√189 = 13,7477 √17 = 4,12310 √116 = 10,7703
Точки образуют треугольник, где MN - большая сторона, а точка К лежит сбоку от неё.
Вот данные об этом треугольнике:
Треугольник MNK (условно назван АВС)
a(ВС) b(АС) c(АВ) p 2p S
4,1231 10,770 13,748 14,320 28,641 17,234
cos A = 0,97253 cos B = 0,79396 cos С = -0,6305
Аrad = 0,2349 Brad = 0,65363 Сrad = 2,2530
Аgr = 13,4609 Bgr = 37,450 Сgr = 129,089.
Відповідь:
1 Высота, проведённая из вершины прямого угла на гипотенузу, есть средняя пропорциональная между отрезками гипотенузы, а каждый катет есть среднее пропорциональное между всей гипотенузой и своей проекцией на гипотенузу. Доказательство. Вот наш прямоугольный треугольник ABC, вот его гипотенуза AB, вот высота CH, проведённая из вершины прямого угла на гипотенузу. И вот отрезки, на которые высота делит гипотенузу: AH и BH. И нам надо доказать, что высота — это среднее пропорциональное между отрезками гипотенузы, то есть AH/CH = CH/BH, доказать, что каждый катет — это среднее пропорциональное между гипотенузой и своей проекцией на гипотенузу, то есть AB/AC=AC/AH и AB/BC=BC/BH. Все эти три равенства следуют из подобия трёх изображённых треугольников ▲ACH, ▲BCH и исходного треугольника ▲ABC.
2
Покрокове пояснення: