Алгоритм таков. Делим 8 монет на з кучки: 2+3+3. Две кучки кладем на чашки весов, две монеты лежат на столе. Если весы остаются в равновесии, то все монеты настоящие. Потом кладем на чашки весов по монете из двух оставшихся. Какая тяжелее, та и фальшивая. Если при первом взвешивании какая-то кучка из 3 монет перевешивает, то в ней находится фальшивка. Делим эту кучку снова на3. Две монеты кладём на чаши весов, сравниваем, какая из них тяжелее. Если они в равновесии, то третья монета фальшивая. В любом случае получается 2 взвешивания.
д)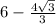 
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
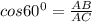
AB=AC·cosn60°=10·1/2=5,
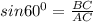
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
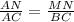или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
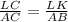или LC=AC·LK/AB=10·2/5=4.
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
Пошаговое объяснение:
1)наверное не 332 а 32
если нет то хз (если мне ответишь ошибка это или нет то я поправлю)
2)
999*999-999*989-9990=999*(999-989)-9990==999*10-9990=9990-9990=0
3)
728*359-628*359+641*1000=
=359*(728-628)+641*1000=
=359*100+641*1000
если и здесь ошибка (не 1000 а 100) то
35900+64100=100000
если нет ошибки то
35900+641000=676900