Формула для приближённого вычисления с дифференциала имеет вид: f(x₀+Δx)≈f(x₀)+d[f(x₀)] По условию задания имеем функцию f(x)=∛x, необходимо вычислить приближённое значение f(8,1)=∛8,1. Число 8,1 представим в виде 8+0,1, то есть х₀=8 Δх=0,1. Вычислим значение функции в точке х₀=8 f(8)=∛8=2 Дифференциал в точке находится по формуле d[f(x₀)]=f'(x₀)*Δx Находим производную функции f(x)=∛x f'(x)=(∛x)'= найдём её значение в точке х₀=8 f'(8)= d[f(8)]=0,0833*0,1=0,0083 Подставляем найденные значения в формулу вычисления с дифференциала и получаем f(8,1)=∛8,1≈2+0,0083=2,0083
ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
Приведем к ступенчатому виду. Применяем операцию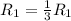 к
к  (к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию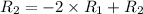 к
к  (ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию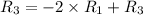 к
к  (к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию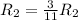 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию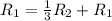 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
Применяем операцию к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию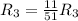 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию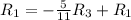 к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию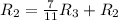 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
Решением является множество упорядоченных пар, которые удовлетворяют системе.