Запишем общую формулу нахождения пути, зная скорость и время:
S = V * t (где S - путь; V - скорость; t - время).
Нам известно, что лодка двигалась по озеру со скоростью 3 5/6 км/ч. Выразим эту неправильную дробь в правильную. Для этого целый показатель умножим на знаменатель, к этому произведению прибавим числитель и разделим всю сумму на знаменатель, а именно:
3 5/6 = (3 * 6 + 5)/6 = (18 + 5)/6 = 23/6.
Время ее пути составило 3 часа.
Найдем, какое расстояние лодка, подставив данные в формулу:
S = 23/6 * 3 = (23 * 3)/6 = 69/6 = 11 3/6 = 11 1/2 = 11,5 (км) - путь, который лодка при этих данных.
ответ: 11,5 километров
1) x₁ = 1,5; x₄ = 2,4; x₉ = 2,7; x₉₉ = 2,97; x₉₉₉ = 2,997;
2) строго возрастает;
3) ограничена.
Пошаговое объяснение:
1) 
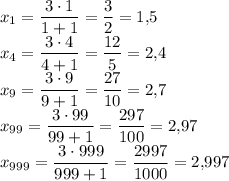
2) Оценим разность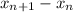 
:
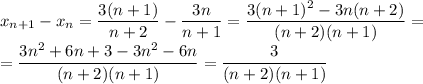
Поскольку n ≥ 1 (как натуральное число), n + 2 > 0, n + 1 > 0. Тогда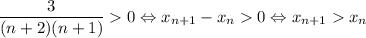 
— каждый следующий член строго больше предыдущего, значит, последовательность строго возрастает.
3) Поскольку последовательность строго возрастает, она ограничена снизу первым членом. Проверим ограниченность сверху:
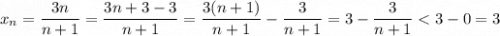
Последовательность ограничена сверху. Поскольку она ограничена и сверху, и снизу, то она ограниченная.
1) 9,88/(6,7-x)=2,6 2) 9,14z-(3,78z+2,87z)=12,45 3)4,6x+3,8x-1,6=0,5
9,88=(6,7-x)*2,6x 9,14z-3,78z-2,87z=12,45 4,6+3,8x=0,5+1,6
9.88=17,42-2,6x 2,49z=12,45 8,4x=2,1
2,6x=17,42-9,88 z=5 x=0,25
x=2,9