7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть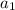 
- изначальное число и 
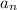- сумма цифр числа 
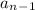. Пусть остаток при делении на 9 у числа 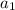- r, тогда и у числа 
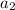остаток при делении на 9 тоже r. Но тогда и у чисел 
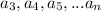остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа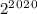 
. А он такой же, как у числа 
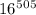, и такой же, как у числа 
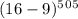, и такой же, как у числа 
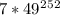, а он такой же, как у числа 
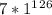, а это равно 7.
а) 60,4 + 12,971 = 73,371
б) 134,143 - 95,4 = 38,743
в) 749,3 * 64,3 = 48179,99
г) 60,3825 : 4,85 = 12,45
д) 269,4+257,135=
+
=
Результаты действий:
а) 73,371 * 100 = 7337,1
б) 38,743 * 100 = 3874,3
в) 48179,99 * 100 = 4817999
г) 12,45 * 100 = 1245
Общая сумма:
7337,1 + 3874,3 + 4817999 + 1245 = 4830455,4
Пошаговое объяснение: С ответом Д я не могу нормально посчитать. Это единственное что получилось