Даны точки A(2; 2) , B(-1; 6), C(-5; 3), D(-2; - 1).
Доказательством, что четырёхугольник АВСД является квадратом, служит равенство сторон и всех углов величине 90 градусов.
Вместо последнего условия можно принять равенство диагоналей.
АВ = √((2 - (-1))² + (2 - 6)²) = √(9 + 16) = 5.
ВС = √(((-1) - (-5))² + (6 - 3)²) = √(16 + 9) = 5.
СД = √((-5) - (-2)²) +( 3) - (-1))²) = √(9 + 16) = 5.
АД = √((2 - (-2))² + (2 - (-1))²) = √(16 + 9) = 5. Стороны равны.
Проверяем диагонали АС и ВД.
АС = √((2 - (-5))² + (2 - 3)²) = √(49 + 1) = √50.
ВД = √(((-1) - (-2))² + (6 - (-1))²) = √(1 + 49) = √50. Они равны.
Заданная фигура - квадрат.
Ну что же, исходим из условия.
Примем количество мальчиков за 
. Тогда весь класс составит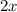 
человек. Тогда отличников в классе всего 
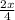(так как 
).
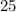Из отличников одна треть - это девочки, а две трети - это мальчики. То есть, девочек в числе отличников всего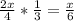 
, а мальчиков в числе отличников: 
.
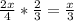Восемь мальчиков отличниками не являются, тогда остальные являются отличниками. Особое внимание на этот вывод - он выводит задачу из относительности в конкретные расчёты.
Такое условие может соблюдаться только при одном равенстве, которое сопоставляет общее количество мальчиков к количеству мальчиков-отличников:
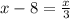
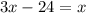
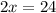
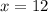
Таким образом, в классе 12 мальчиков, 12 девочек и 24 ученика в классе.
----
Предлагаю проверить задачу по условию.
В классе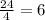 
отличников. Треть из них - девочки, значит, в классе 
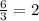отличницы и 
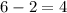отличника. Восемь мальчиков в число отличников не входят: прибавив 8 к 4, получаем общее количество мальчиков в классе: 12.
По смыслу также подходит, решение подтверждено.
ответ:дпднгкмеусыцчй3ц5а58мкми
какаято бредятина
Пошаговое объяснение: