ответ Чтобы представить смешанное число в виде неправильной дроби, нужно знаменатель умножить на целую часть числа, к полученному произведению прибавить числитель дробной части и записать эту сумму в числитель дроби. В знаменатель неправильной дроби записываем знаменатель дробной части смешанного числа.
знаменатель у нас -15
целое чило-4
числитель-7
15×4+7=67 это будет чилитель неправильной дроби
а знаменатель неправильной дроби записываем знаменатель дробной части смешанного числа-15
Представим смешанное число в виде неправильной дроби 4 7/15= 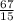
Пошаговое объяснение:
Решение задач :
Задача № 1 :
Преобразуем уравнение к следующему виду: (х – 2006)(у - 2006) = 20062.
Уравнение имеет решения, например, х = у = 4012.
Задача № 2 :
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π,
и применяя формулы: cos2x = (1 + cos2x)/2, cosx = - cos(π - x), cosx + cosy = (2cos((x + y)/2))cos((x - y)/2),
получим справедливое тождество. Задача № 4 :
Пусть y = x2 – 3x3. Тогда y' = 2x – 9x2 и с метода интервалов получаем, что y' < 0 при всех x>2/9.
Но 1/4>2/9, следовательно, функция y(x) убывает на луче [1/4; +∞].
Это значит, что x2 - 3x3 < 1/16 - 3/64 = 1/64 < 1/64.
Задача № 5 :
Окружим каждый квадрат полоской шириной 1/2.
Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4.
Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500.
Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям.
Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов.
1) - неверно, так как если бы каждый ученик посещал оба кружка, то в каждом кружке было бы по 20 человек, а это не так.
2) - неверно, так как на историю ходит 13 человек, а на математику 10, то есть минимум 3 ученика ходят на кружок истории, но не посещают математику (может и больше, но минимум - 3).
3) - верно, так как больше половины класса задействованы на кружке истории и половина - на кружке математики. То есть, даже если все 20 человек посещают эти кружки, то хотя бы трое их них всё равно окажутся и там, и там.
4) - верно, так как математику посещают только 10 человек.
То есть, правильными оказываются утверждения