ответ:x =i
Пошаговое объяснение: Пусть число z=x + iy
– искомое комплексное число, где x и y – действительные числа. Тогда число z⁻= x - iy , сопряженное числу z
По условию задачи имеем:z⁻ = z³ , ⇒ (x+iy)³= x - iy ⇒
x³+3x²iy+3xi²y²+i³y³= x - iy
Преобразовав это уравнение, получим: (x³+3x²y)+ i(3x²y-y³)= x-iy
У нас два комплексных числа равны , значит будут равны соответственно их действительные и мнимые части:
x³+3x²y=х и 3x²y-y³= -у
Возможны два случая: 1) если у≠0, то
x³+3xy²=х и 3x²-y²= -1
у² =1+3х² ⇒
х³+3х(1+3х²)=х ⇒ 10х³ + 2х=0 ⇒ 2х(5х²+1) = 0 ⇒ х =0, тогда у=1+3·0²=1 Этот случай имеет следующее решение: (0; 1)
Тогда число z₁=0+1·i = i ⇒ z₁= i искомое комплексное число
2) если у=0, то
х³ - х =0 и у = 0
х(х² -1) =0
х=0 или х=±1
Этот случай имеет следующие решения: (0; 0) и (1; 0), (-1; 0)
тогда им соответствуют числа
z₂=0+0·i = 0 ( действительное число)
z₃= 1+0·i = 1 ( действительное число)
z₄=-1+0i= -1 ( действительное число)
Значит х = i -искомое комплексное число
0, 1, -1, i, -i.
Пошаговое объяснение:
Для числа a+bi сопряженное a-bi. Получаем (a+bi)^3 = a-bi;
a^3 + 3 a^2 bi + 3 a (bi)^2 + (bi)^3 = a - bi
a^3 + 3 a^2 bi - 3 a b^2 - b^3 i = a - bi
Действительные и мнимые части должны совпадать:
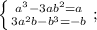если a и b не равны 0, то
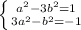
Складываем уравнения: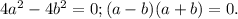 
Отсюда a=b или a = -b. В любом из этих случаев из первого уравнения 
, что невозможно.
Если a=0, то из второго уравнения (до сокращения)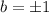 
или b = 0.
Если b=0, то из первого уравнения 
или a = 0.
Итого 5 чисел: 0, 1, -1, i, -i.
1) х = 3
2) х = 1,7
3) х = 9,9
4) а = 5
5) y = 8
6) y = 2
7) y = 4
пошаговое объяснение:
1) 3 • (2х - 1) - 3х = 6
6х -3 - 3х = 6
3х = 6 + 3
3х = 9
х = 9/3
х = 3
2) -(0,7 - 3х) = 4,4
-0,7 +3х = 4,4
3х = 4,4 + 0,7
3х = 5,1
х = 5,1/3
х = 1,7
3) 2х + 7 • (х - 5,8) -3х = 18,8
2х + 7х - 40,6 - 3х = 18,8
6х = 18,8 + 40,6
6х = 59,4
х = 59,4/6
х = 9,9
4) 4а - (2а - 15) = 25
4а - 2а + 15 = 25
2а = 25 - 15
2а = 10
а = 10/2
а = 5
5) 11 • (y - 3) -10y = -25
11y - 33 - 10y = -25
y = -25 + 33
y = 8
6) 0,5 • (8y + 6) - 2y = 7
4y + 3 - 2y = 7
2y = 7 - 3
2y = 4
y = 4/2
y = 2
7) 1,2y - 0,6 • (y - 3) = 4,2
1,2y - 0,6y + 1,8 = 4,2
0,6y = 4,2 - 1,8
0,6y = 2,4
y = 2,4/0,6
y = 4