Если бы была картинка то можно было бы и сказать, а так если без картинки, то наверное повернуть 3 раза на право или три раза на лево
Пошаговое объяснение:
(если не сложно, сделай лучшим ответом)
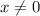
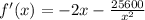
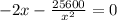
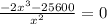
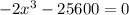
![x = \sqrt[3]{-12800}](/tpl/images/0576/3504/338d2.png)
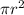, можно найти 
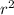=9 => r=3. Если у нас один из катетов равен 3, а гипотенуза равна 5, то, вспоминая египетский треугольник, можно узнать величину другого катета - 4. Это и есть x, но это только половина высоты => вся высота равна 8. Зная площадь основания и высоту, можно найти V=S*h=9
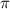*8=9*3*8=216.
