1. Пусть в одном куске - x м полотна, тогда во втором - х+7 м. Всего 23 м. Составим и решим уравнение: x+x+7=23 2x=23-7 2x=16 x=16/2 x=8 м - в первом куске полотна. 8+7=15 м - во втором куске.
ответ: 8 и 15 м.
2. Найдите значение выражения 3x-2 при x=1 2/3. х=1 2/3=5/3 3*5/3-2=5-2=3.
ответ: 3.
3. Упростите выражение 2x-3-(5x-4). 2x-3-(5x-4)=2х-3-5х+4=-3х+1
ответ: -3х+1.
4. Зависит ли от значения x значение выражения: 3(2x-1)-2(5x-4)-(2-4x)? 3(2x-1)-2(5x-4)-(2-4x)=6х-3-5х+4-2+4х=5х-1
ответ: Да, от значения х зависит значение выражения.
Для наглядности удобно провести некоторое соответствие с трехмерным пространством
Понятно что z(x,y) можно в нем изобразить как некоторую поверхность
Точке (1,4) соответствует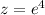
, т.е. точка 
(*)
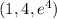Линию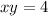
удобнее записать как трехмерную кривую 
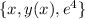, что будет пересекать поверхность z(x,y) при x=1
Запишем уравнение касательной к этой кривой в точке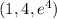
, в качестве параметра берем переменную x
(вычисляется по аналогии с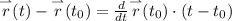
)
В прикрепленном файле нарисована поверхность, кривая и касательная.
Зная уравнение касательной, построим единичный вектор в направлении убывания x:
Пусть x=0, тогда из (#) получим точку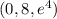
Соотв. единичный вектор в направлении этой точки из (*) имеет вид
Понятно что z компонента никак не повлияет на значение производной по направлению, формально вектор можно записать как
И, наконец, найдем искомую производную: