Раз область значений функций левой и правой части уравнения , то, приравняв левую и правую части уравнения к нулю, получим и откуда и - одно решение
Левая часть - под коренное выражение неотрицательно, т.е. уравнение будет зависеть только от правой части.
Возводим левую и правую части уравнения в квадрат
При условии, что , возводим снова в квадрат обе части уравнения:
В левой части применим формулу разности квадратов:
Произведение равно нулю, если хотя бы один из множителей равен нулю.
откуда
откуда
Теперь исследуем на условии . Подставляем первый корень
Решением этого неравенства является промежуток
Подставим теперь второй корень.
решением этого неравенства является промежуток
Пересечение этих двух решений: . Из выше сказанного при а = -0,5 уравнение имеет одно решение. Поэтому при данное уравнение имеет более одного решения.
Половина из этого набора чисел - четные. Исключим их, в итоге останется ровно 500 чисел. Теперь определим, сколько чисел x, соответствующих условию. Наименьшее из таких чисел 1, а наибольшее 997. При этом, если не брать в учет четные числа (т.к. мы их исключили), то начиная с 1 они возрастают на 6 единиц, т.е 1, 7, 13, ... , 997. С формулы нахождения кол-ва членов ариф. прогрессии, посчитаем сколько всего таких чисел.
Формула: n=(An-A1)/d +1 где An-последний член; A1-первый член; d-разность.
Раз область значений функций левой и правой части уравнения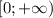 , то, приравняв левую и правую части уравнения к нулю, получим
, то, приравняв левую и правую части уравнения к нулю, получим 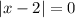 и
и 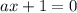 откуда
откуда 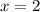 и
и  - одно решение
- одно решение
Левая часть - под коренное выражение неотрицательно, т.е. уравнение будет зависеть только от правой части.
Возводим левую и правую части уравнения в квадрат
При условии, что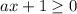 , возводим снова в квадрат обе части уравнения:
, возводим снова в квадрат обе части уравнения:
В левой части применим формулу разности квадратов:
Произведение равно нулю, если хотя бы один из множителей равен нулю.
Теперь исследуем на условии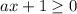 . Подставляем первый корень
. Подставляем первый корень
Решением этого неравенства является промежуток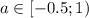
Подставим теперь второй корень.
решением этого неравенства является промежуток![a \in (-\infty;-2]\cup(-1;+\infty)](/tpl/images/0922/4683/afe62.png)
Пересечение этих двух решений: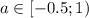 . Из выше сказанного при а = -0,5 уравнение имеет одно решение. Поэтому при
. Из выше сказанного при а = -0,5 уравнение имеет одно решение. Поэтому при  данное уравнение имеет более одного решения.
данное уравнение имеет более одного решения.
ответ: при a ∈ (-0.5;1).