1) 3/5 + 2 4/5 = 2 7/5 = 3 2/5
2) 8 - 6 9/10 = 7 10/10 - 6 9/10 = 1 1/10
3) 1 4/9 - 5/9 = 13/9 - 5/9 = 8/9
4) 8 2/7 - 3 4/7 = 7 9/7 - 3 4/7 = 4 5/7
5) 3 12/17 + 2 6/17 = 5 18/17 = 6 1/17
6) 7 5/9 - 6 7/9 = 6 14/9 - 6 7/9
7) 9/13 + 7/13 = 16/13 = 1 3/13
8) 8 8/13 + 6 5/13 = 14 13/13 = 15
9) 1 3/5 - 4/5 = 8/5 - 4/5 = 4/5
10) 7/11 + 8/11 = 15/11 = 1 4/11
11) 6 4/9 - 4 = 2 4/9
12) 5 9/17 + 7 12/17 = 12 21/17 = 13 4/17
13) 1 8/13 - 9/13 = 21/13 - 9/13 = 12/13
14)10/16 + 9/16 = 19/16 = 1 3/16
15) 8 3/11 - 7 5/11 = 7 14/11 - 7 5/11 = 9/11
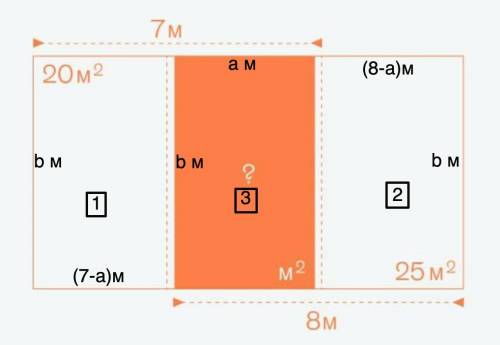
Площадь маленького прямоугольника внутри большого прямоугольника равна 15 м².
Пошаговое объяснение:
Надо найти площадь маленького (оранжевого) прямоугольника внутри большого.
Вспомним формулу площади прямоугольника:
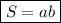, где а и b - ширина и высота прямоугольника.
Обозначим ширину искомого прямоугольника №3 - а м, высоту - b м
⇒ 
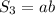
Тогда ширина прямоугольника №1 - (7-а) м,
а прямоугольника №2 - (8-а) м.
Высоты этих прямоугольников равны - b м.
А площади этих прямоугольников будут соответственно равны:
Для того, чтобы найти искомую площадь, надо найти ширину и высоту прямоугольника №3.
1. Выразим b из площади прямоугольника №1:
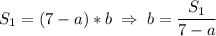
Подставим значение площади S₁ = 20 м² в полученное выражение:
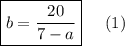
2. Выразим b из площади прямоугольника №2:
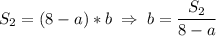
Подставим значение площади S₂ = 25 м² в полученное выражение:
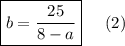
3. Приравняем выражения (1) и (2) и найдем а.
Воспользуемся основным свойством пропорции:
Произведение крайних членов равно произведению средних членов.
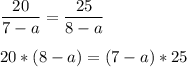
Раскроем скобки. Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный и решим уравнение:
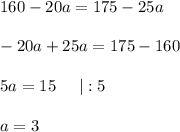
⇒ ширина маленького прямоугольника равна 3 м.
4. Подставим значение а=3 в (1) или (2) равенства и найдем b.
Подставим в (1):
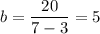
⇒ высота маленького прямоугольника равна 5 м.
5. Теперь, зная ширину и высоту, можем найти площадь маленького прямоугольника №3:
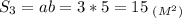
⇒ Площадь маленького прямоугольника равна 15 м².
∛z=∛-1=-1
Пошаговое объяснение:
-1*-1*-1=-1
∛-1=-1