1) 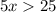
Обе части неравенства делим на положительное число 5, поэтому знак неравенства не изменится.
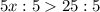
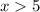
ответ: (5; +∞)
2) 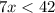
Решаем так же.
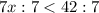
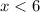
ответ: (-∞; 6)
3) 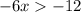
Обе части неравенства делим на отрицательное число (-6), поэтому знак неравенства изменится на противоположный.
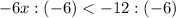
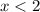
ответ: (-∞; 2)
4) 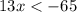
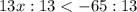
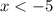
ответ: (-∞; -5)
5) 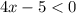
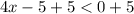
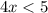
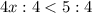
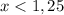
ответ: (-∞; 1,25)
6) 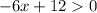
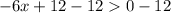
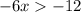
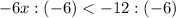
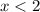
ответ: (-∞; 2)
7) 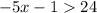
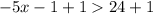
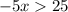
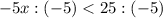
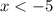
ответ: (-∞; -5)
8) 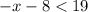
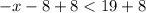
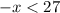
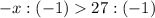
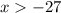
ответ: (-27; +∞)
Пошаговое объяснение:
x² - 5*x + 6 = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = -5² - 4*(1)*(6) = 1 - дискриминант. √D = 1.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (5+1)/(2*1) = 6/2 = 3 - первый корень
x₂ = (-b-√D)/(2*a) = (5-1)/(2*1) = 4/2 = 2 - второй корень
3 и 2 - корни уравнения - нули функции..
Область определения функции - Х≠ 3.
В числителе разложим на множители.
y = (x-1)*(x-2)*(x-3)/(x-3) и сокращаем (х - 3).
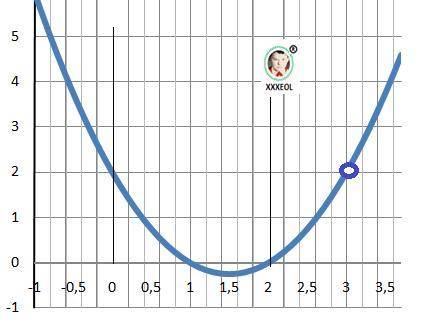
Получилась парабола
у = (х-1)*(х-2) = х² - 3*х + 2 - строим график.
Рисунок с графиком - в приложении.
При Х = 3 - разрыв 1-го рода - "дырка"
Пошаговое объяснение:
Задача 1.
1.5*(b+5)*b = (b+6)*(b+1) - прибавили по 1 м и стал в 1,5 раза больше.
1,5*b² + 7.5*b = b² + 7*b + 6
0.5*b² - 0.5*b - 6 = 0
D = 12.25, и два корня b₁ = 3, b₂ = -4
b = 3 м - ширина
a = b + 5 = 3 + 5 = 8 м - длина
Периметр по формуле:
P = 2*(a+b) = 2*(8 + 3) = 22 м - периметр - ответ.
Второе решение b₂ = 4 - это у измененного прямоугольника.
Задача 2.
Периметр параллелограмма
P = 2*(a+b) = 66 см
a + b = 33 см
a = 33 - b
Площадь параллелограмма по формуле:
S = a*h = a*(80%*b) = 216 см²
a*b = 216 : 0.8 =270
a = 33 - b
(33 - b)*b = 370
- b² + 33*b - 270 = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = 33² - 4*(-1)*(-270) = 9 - дискриминант. √D = 3.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (-33+3)/(2*-1) = -30/-2 = 15 - первый корень
x₂ = (-b-√D)/(2*a) = (-33-3)/(2*-1) = -36/-2 = 18 - второй корень
b = 15 см и а = 18 см - стороны параллелограмма - ответ..
Пошаговое объяснение:
1.x>25:5
x>5
2.x<42:7
x<6
3.-x>2
4.x<-5
5.4x<5
x<4/5
6.12<6x
2<x
7.-5x>24+1
-5x>25
25<5x
5<x
8.-x<19+8
-x<27
27>x