ответ: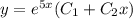
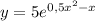
Пошаговое объяснение:
Определить общее решение дифференциального уравнения:
y" - 10y' + 25y = 0.
Решение
Характеристическое уравнение имеет вид:
k² - 10k + 25 = 0
(k - 5)² = 0
k₁ = k₂ = 5
Корни действительные и равные k₁ = k₂ = k . В этом случае общее решение уравнения:
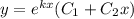
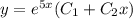
Определить частное решение дифференциального уравнения:
y'+y=xy, удовлетворяющее начальному условию y(2)=5.
Решение
y' + y = xy
y' = xy - у
Делим обе части уравнения на у
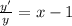
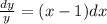
Интегрируем обе части уравнения
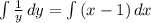
ln|y| -lnC = 0.5x² - x
Запишем общее решение ДУ
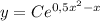
Найдем частное решение ДУ подставив начальные условия y(2)=5
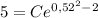
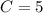
Поэтому частное решение ДУ
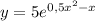
составим пропорцию
а) 27 м - х %
340 м - 100%
от сюда 27* 100 : 340 = (с округлением до сотых) 7,94%
б) 4700 м - 100% (1км = 1000м // 4,7 *1000 = 4700)
998 м - х %
х = 998 * 100 : 4700 = (с округлением) 21,23%
в) 1700 г - 100% (1 кг = 1000 г // 1,7 * 1000 = 1700)
12 г - х %
х = 12 * 100 : 1700 = (с округлением) 0,71%
г) не знаю, что обозначают эти единицы измерения?
Е) 1 ГА - 0,01 км2
значит, в 7890 ГА - 78,9 км2
составим пропорцию 78,9 км2 - х %
1 км2 - 100 %
значит, х = 78,9 * 100 : 1 = 7890 %
запишим это по другому: в 7890 га - 78,8 км2
в 100 га - 1 км2
y=61 км/ч
x=91.5 км/ч
z=183 км(вдруг пригодится)
Пошаговое объяснение:
Скорость автобуса:у
Скорость машины:х
Расстояние:z
х=у+30.5
z=2x
z=3y
2x=3y
2y+61=3y
y=61 км/ч
x=91.5 км/ч
z=183 км