а) (2; 16) и (3; 19)
б) (1; 1)
Пошаговое объяснение:
Для того что б найти их точку пересечения нужно их приравнять.
а) y = x² та y = 5x + 6
x² = 5x+6
x² - 5х + 6 = 0
Дискриминант:
D = 25 - 4 * 1 * 6 = 25 - 24 = 1
x₁ = 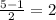
x₂ = 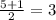
Для того что б теперь найти у достаточно просто подставить х во вторую функцию:
у₁ = 5 * 2 + 6 = 16
у₂ = 5 * 3 + 6 = 19
Поскольку первый график это парабола то точки пересечения - две:
(2; 16) и (3; 19)
б) Тоже приравниваем:
y = 4 x - 3 та y = - x + 2
4x - 3 = -x + 2
5х = 5
х = 1
Подставляем в любую функцию:
y = -х + 2
у = -1 + 2
у = 1
(1; 1)
ответ: Из 1-го уравнения следует: х-3=0 или у+5=0, т е x=3 или у=-5,
далее из 2-го ур-я: у-6=11(х+у-7), при условии, что х+у-7 не равно нулю.
Получаем у-6 = 11х+11у-77, 11х+10у=71, (х + у) не равно 7.
Система разбивается на такие случаи:
а) х=3, тогда 11*3 + 10у=71, откуда 10у= 38, у=3,8
б) у=-5, тогда 11х+10*(-5)=71, откуда 11х=121, х=11
эти пары не дают в сумме 7, значит они являются решениями системы.
С другой стороны пара (3;-5) не явл. решением, т.к при подстановке
х=3, у=-5 во второе уравнение исходной системы равенства нет.
ответ: (3; 3,8), (11; -5)
4(3/8)%=3/200=0,015