Как видим, таких критических точек - множество. Определим некоторые из них, которые принадлежат отрезку . Для этого будем брать всевозможные целые значения
Пусть . Тогда
Пусть . Тогда
Только одно значение , при котором данные критические точки входят в промежуток
Итак, только на одном из трех вариантов: заданная функция может принимать наименьшее значение. Вычислим ее значение в этих трех точках, зная их абсциссы, и найдем наименьшее:
Если , то
Если , то
Если , то
Для того чтобы определить наименьшее из трех, можно подставить приблизительное значение числа , а именно 3,14. Видим, что наименьшим значением функции является точка
Х было Х:2= 1/2х взял Саша Х-1/2х=1/2х осталось 1/2х:2=1/2х• 1/2= 1/4х взял Кирилл 1/2х -1/4х= (1•2)/(2•2)х- 1/4х= 2/4х-1/4х= 1/4х осталось 1/4х :2= 1/4х•1/2=1/8х взяла Света 1/4х- 1/8х= (1•2)/(4•2)х- 1/8х= 2/8х - 1/8х= 1/8х осталось и это 3 конфеты
1/8х = 3 Х= 3:1/8 Х= 3• 8/1 Х= 24 конфеты
ответ: в коробке было (А) 24 конфеты
Без икс решаем сконца
3 осталось как взяла света и это половина 1)) 3•2=6 к было до того как света взяла
6к взял Кирилл и это половина остатка
2)) 6•2=12 к было до того как Кирилл взял
и это половина всех конфет
3)) 12•2=24 к всего было ОТВЕТ
Выражением 3•2•2•2=24к
Проверка 24:2=12к взял Саша 24-12=12 к осталось 12/2=6 взял Кирилл 12-6=6 к осталось 6:2=3 к взяла света 6-3=3 к осталось
Найдем критические точки функции:
Как видим, таких критических точек - множество. Определим некоторые из них, которые принадлежат отрезку![\bigg[0; \ \dfrac{\pi}{2} \bigg]](/tpl/images/1053/3544/bcfb7.png) . Для этого будем брать всевозможные целые значения
. Для этого будем брать всевозможные целые значения 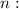
Пусть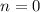 . Тогда
. Тогда ![x = (-1)^{0} \cdot \dfrac{\pi}{3} + \pi \cdot 0 = \dfrac{\pi}{3} \in \bigg[0; \ \dfrac{\pi}{2} \bigg]](/tpl/images/1053/3544/ba189.png)
Пусть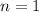 . Тогда
. Тогда ![x = (-1)^{1} \cdot \dfrac{\pi}{3} + \pi \cdot 1 = -\dfrac{\pi}{3} + \pi = \dfrac{2\pi}{3} \notin \bigg[0; \ \dfrac{\pi}{2} \bigg]](/tpl/images/1053/3544/5bc2a.png)
Только одно значение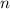 , при котором данные критические точки входят в промежуток
, при котором данные критические точки входят в промежуток ![\bigg[0; \ \dfrac{\pi}{2} \bigg]](/tpl/images/1053/3544/bcfb7.png)
Итак, только на одном из трех вариантов: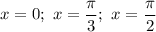 заданная функция может принимать наименьшее значение. Вычислим ее значение в этих трех точках, зная их абсциссы, и найдем наименьшее:
заданная функция может принимать наименьшее значение. Вычислим ее значение в этих трех точках, зная их абсциссы, и найдем наименьшее:
Если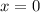 , то
, то 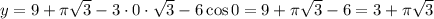
Если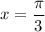 , то
, то 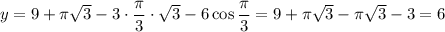
Если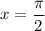 , то
, то 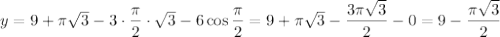
Для того чтобы определить наименьшее из трех, можно подставить приблизительное значение числа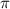 , а именно 3,14. Видим, что наименьшим значением функции является точка
, а именно 3,14. Видим, что наименьшим значением функции является точка 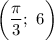
ответ:![\underset{[0; \frac{\pi}{2} ] }{\min y} = y\bigg(\dfrac{\pi}{3} \bigg) = 6\\](/tpl/images/1053/3544/e0787.png)