ответ:л
Пошаговое объяснение:
Чтобы из числа можно было сделать все шесть различных двухзначных чисел, необходимо, чтобы исходное число было трехзначным и все цифры в нем были разные, представим это число в виде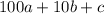 
.
А сумма всех шести различных двухзначных чисел будет такая:
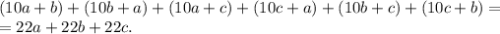
При этом (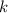
натуральное):
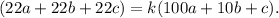
Представим теперь, что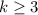 
, то есть:
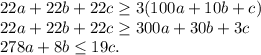
Но это противоречие, так как правая часть по-любому больше левой, а здесь она меньше. Поэтому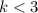 
.
Итак, нужно рассмотреть два случая:
1). 
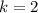. Тогда:
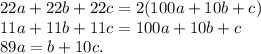
Нетрудно понять, что в натуральных однозначных числах здесь всего одно решение: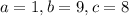 
.
А нужное число - это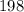 
.
2). Случай посложнее: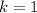 
.
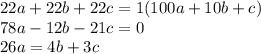
Если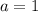 
уравнение принимает вид 
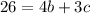, и, тогда в вышеуказанных условиях у него такое одно решение: 
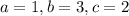. Число - 
.
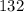Ну а теперь пусть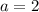 
и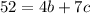 
. Здесь методом подбора: 
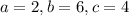. А число - 
.
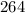И последний случай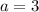 
, то есть 
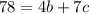, где, подбором, 
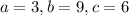. Число 
.
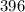Делаем вывод, что Вася богатый и у него в доме четыре (по крайней мере!) квартиры.
Пошаговое объяснение:
Введем такую функцию f(x) = 16x^4 - 64x + 31. Теперь нужно доказать что f (x) проходит через ось Х на интервале (0:1) не больше 1 раза.
Найдём f'(x) = 64x^3 - 64. Найдём где функция убывает и возрастает. То есть нужно прировнять к 0 производную. 64x^3 - 64 = 0
x = 1.
То есть до точки 1 функция убывает, а после возрастает -> функция непрерывна поэтому максимум 1 точка пересечения с осью оХ на интервале (0;1)
Если интересно узнать имеет ли хоть 1 корень то нужно узнать f (0) = 31 и f (1) < 0 -> имеет точку пересечения
коэффициент это
Пошаговое объяснение:
Если выражение является произведением числа и одной или
нескольких букв, то это число называют числовым коэффициентом
(или просто коэффициентом).
Например: 5 • а = 5а ; 5 — коэффициент.
Коэффициент обычно пишут перед буквенными множителями.
Коэффициентом такого выражения, как а или аb , считают 1 ,
так как:
а = 1 • а = 1а; ab = 1 • ab = 1ab.
При умножении –1 на любое число а получается число –а .
–1 • a = –1a = –а.
Поэтому числовым коэффициентом выражения –a считают число –1 .