608 * 25 =15200
83 * 56 =4648
165 * 27 = 4455
333 * 65 =21645
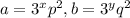, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
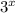, получим уравнение 
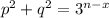. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 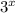, имеем 
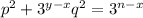. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
Дохристианская Русь гражданский новый год начинала 1 марта. Зима закончилась - Новый год, пора готовиться к новым посевам.
В 15 веке Русь официально начинает праздновать его 1 (14) сентября. Оно и выстраивалось логично – урожай собран, работы завершены. Начинается новый год.
Новый год праздновали 1 сентября до тех пор, пока великий реформатор Петр I не захотел внести изменения в календарь. В 1699 г. Петр повелел отмечать Новолетие 1 января, как это было принято в Европе.
Церковная традиция отмечать Новолетие 1 сентября сохранилась и до сегодняшнего дня.
1 (14) сентября Церковь празднует начало индикта, или церковного Новолетия. Решение начинать Новый год 1 сентября (по ст. ст.) было принято на I Вселенском соборе в 325 г. Считается, что это было сделано в память о том, что в 312 (313) г. византийский император Константин Великий даровал христианам полную свободу исповедовать свою веру. Из Византии на Русь пришла традиция называть Новолетие началом индикта.
Кроме этого в ветхозаветной церкви месяц сентябрь праздновался ежегодно, в ознаменование покоя от всех житейских забот.
608 * 25 =15200
83 * 56 =4648
165 * 27 = 4455
333 * 65 =21645