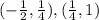ответ:1)~ (3a-1)^3-27a^3+5=(3a-1)^3-(3a)^3+5=(3a-1-3a)\cdot\\ \\ \cdot((3a-1)^2+3a\cdot(3a-1)+(3a)^2)+5=-(9a^2-6a+9a^2+1+9a^2-3a)+\\ \\ +5=-27a^2+9a+4
Если а=-1, то -27a^2+9a+4=-27\cdot(-1)^2+9\cdot(-1)+4=-32
Если а=0, то -27a^2+9a+4=-27\cdot0^2+9\cdot0+4=4
Если а=1, то -27a^2+9a+4=-27\cdot1^2+9\cdot1+4=-14
2)~ (0.7b-2)^3-(0.7b+2)^3=(0.7b-2-0.7b-2)((0.7b-2)^2+\\ \\ +(0.7b-2)(0.7b+2)+(0.7b+2)^2)=-4(0.49b^2-2.8b+4+0.49b^2-\\ \\ -4+0.49b^2+2.8b+4)=-4(1.47b^2+4)=-5.88b^2-16
Если а=-2, то -5.88b^2-16=-5.88\cdot(-2)^2-16=-39.52
Если а=-1, то -5.88b^2-16=-5.88\cdot(-1)^2-16=-21.88
Если а=1, то -5.88b^2-16=-5.88\cdot1^2-16=-21.88
(5x-4)^3+(5x-2)^3-250x^3=125x^3-300x^2+240x-64+125x^3-\\ \\ -150x^2+60x-8-250x^3=-450x^2+300x-72
Если x=0.5, то -450x^2+300x-72=-450\cdot0.5^2+300\cdot0.5-72=-147
Если x=0, то -450x^2+300x-72=-450\cdot0^2+300\cdot0-72=-72
(0.2+5y)^3-(0.5+2y)^3-117y^3=125y^3+15y^2+0.6y+0.008-8y^3-\\ \\ -6y^2-1.5y-0.125-117y^3=9y^2-0.9y-0.117
Если y=-1, то 9y^2-0.9y-0.117=9\cdot(-1)^2-0.9\cdot(-1)-0.117=9.783
Пошаговое объяснение:
ответ: Увеличение на: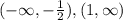
Убывает на: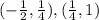 .
.
Пошаговое объяснение: Найдем производную.
Приравняем производную к 0.
Решим относительно x.
Упростим числитель.
Найдем НОЗ членов уравнения.
Умножим каждый член на и упростим.
и упростим.
Решим уравнение.
Разлагаем на множители левую часть уравнения.
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
Приравняем x-1 к 0, затем решим относительно x.
Приравняем 2x+1 к 0, затем решим относительно x.
Решение является результатом x-1=0 и 2x+1=0.
Значения, которые обращают производную в 0 - 1, .
.
1, .
.
Выясним, при каких значениях переменной функция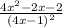 не определена.
не определена.
Разобьем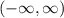 на интервалы вокруг значений x, в которых производная равна 0 или не определена.
на интервалы вокруг значений x, в которых производная равна 0 или не определена.
Подставим значение из интервала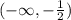 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на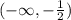 , так как
, так как 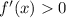 .
.
Подставим значение из интервала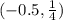 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Убывает на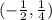 , поскольку
, поскольку 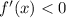
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Убывает на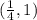 , поскольку
, поскольку 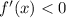
Подставим значения из интервала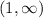 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на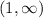 , так как
, так как 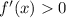 .
.
Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на: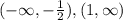
Убывает на: