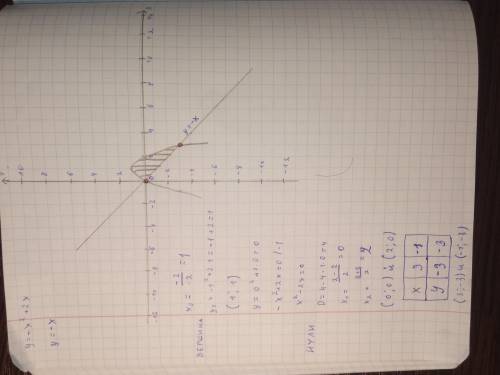
Сперва рисуем два графика и находим фигуру, которая появляется при их пересечении. Как мы это сделали - смотри на фото.
Число 0 будет нижним пределом интегрирования (ибо самая "левая" точка пересечения графиков (0; 0) (смотрим по х) ), а 3 - верхним (ибо самая "самая" правая точка пересечения - (3;-3), опять же, смотрим по х).
Дальше приравняем две функции:
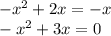
Теперь площадь фигуры можно найти через определённый интеграл:
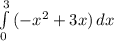
Найдём для начала неопределённый интеграл:
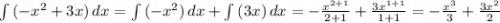
Теперь подставим пределы интегрирования:
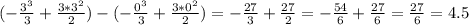
S = 4.5
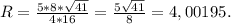
20%=0,2
114%=1,14
8,6%=0,086
0,301=30,1%
0,87=87%
0,9=90