ответ: прямоугольный треугольник это треугольник у которого один угол равен 90 градусов. (Он называется прямым).
Первое свойство прямоугольного треугольника: в прямоугольном треугольнике сумма острых углов равна 90 градусов. Второе свойство прямоугольного треугольника: катет лежащий против угла в 30 градусов равен половине гипотенузы. 3 свойства прямоугольного треугольника: если катет прямоугольного треугольника равен половине гипотенузы, то угол лежащий против этого катета равен 30 градусов.
Приведу вместо свойства гипотенузы свойство медианы проведенной из вершины прямого угла:. в прямоугольном треугольнике медиана проведенная из вершины прямого угла равна половине гипотенузы. если медиана треугольника равна 1/2 стороны к которой она проведена то этот треугольник прямоугольный.
Количество отрезков равно количеству комбинаторных сочетаний (ведь порядок вершин не важен) из 5 по 2:
(первое фото)
Чтобы обозначить все отрезки, можно использовать такой алгоритм. Сначала берём первую букву (самую левую) и объединяем с четырьмя оставшимися: PD, РМ, РТ, PS
Далее берём вторую букву слева. Сочетаем их только с буквами, стоящими справа, так как с первой буквой мы уже соединили в первом действии: DM, DT, TS. Третью букву: MТ, MS Четвёртую букву: TS.
В сумме получаем десять отрезков:(второе фото)
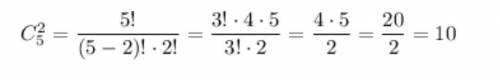
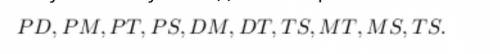
Сначала обратим внимание на разновидность данной функции. От вида функции будет зависеть внешний вид кривой графика. Другими словами, определим, будет это прямая, парабола или что-нибудь еще.
В этом конкретном случае функция, заданная в условии, является линейной, соответственно ее график будет представлять собой прямую линию. Эти данные уже несколько упрощают наше задание.
Для построения прямой линии абсолютно достаточным является построение двух точек этой прямой, через которые и проведем прямую.
Найдем такие точки, через которые будет проходить заданная прямая. Для этого должно выполняться равенство:
у = х – 3.
Подставим в это равенство два абсолютно произвольных значения для переменной х, так как прямая является бесконечной и будет иметь соответствующие значения функции для любого аргумента. Для примера выберем значения –1 и 1.
При х = –1 найдем значение функции:
у(–1) = –1 – 3 = –4
у(1) = 1 – 3 = –2
получили две точки (–1; –4) и (1; –2). Нанесем их на координатную плоскость и проведем прямую, которая будет описываться уравнением у = х – 3.
Пошаговое объяснение: