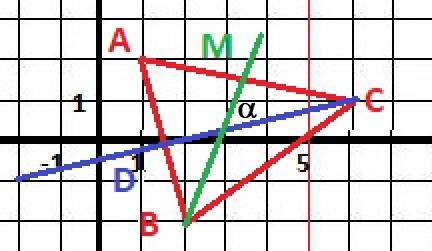
Дано: А(1;2), B(2;-2), C(6;1)
Найти: α - CD,BM
Пошаговое объяснение:
1. Находим уравнение перпендикуляра CD к стороне АВ.
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(2--2)/(1-2)=-4 - наклон прямой
2) b=Аy-k*Аx=2-(-4)*1=6- сдвиг по оси ОУ
Уравнение Y(АВ) = -4*x+6
Наклон перпендикуляра - k2 = - 1/(-4) = 1/4 = 0.25
Точка C(6,1), наклон - k2 = 0,25
b = Cу - k*Cx = 1 - (0,25)*6 = -0,5
Уравнение высоты - Y(CD) = 0,25*x - 0,5
2. Находим уравнение медианы ВМ.
Находим координаты точки М = (А+С)/2
Мх = (1+6)/2 = 3,5, Му = (2+1)/2 = 1,5.
Находим уравнение медианы ВМ через точку В(2;-2) и М(3,5;1,5)
1) k = ΔY/ΔX = (Мy-Вy)/(Мx-Вx)=(1,5--2)/(3,5-2)=2 1/3 - наклон прямой
2) b=Мy-k*Мx=1,5-(2 1/3 * 3,5= -6 2/3- сдвиг по оси ОУ
Уравнение медианы Y(МВ) = 2 1/3*x - 6 2/3
3. Расчет угла между двумя прямыми. k1 = 2 1/3, k2 = 1/4
tgα = (k2 - k1)/(1 + k1*k2)
k2 - k1 = 2 1/12 = 2,083
1 + k1*k2 = 1 7/12 = 1,583
tg α = 1 6/19 = 1,316
α = 0.921 рад = 52.77° - ОТВЕТ
70:(-10)=-7
2-7=-5
65-74=9
5*(-9)=-45
-5+6*(-3)-81:9
6*(-3)=-18
-81:9=9
-5+(-18)=-13
-13-9=-22
76-(8*(-8)-30:6
8*(-8)=-64
30:6=5
-64-5=59
76-59=17
7*(-3-6)-50:(-10)
-3-6=-3
7*(-3)=-21
50:(-10)=-5
-21-(-5)=26
(-89+78+3*(-7))*4
3*(-7)=-21
-89+78=167
-21+167=188
188:4=47
(-8+8:(-4))*91-88
8:(-4)=-2
-8+(-2)=-6
91-88=3
-6*3=18
49-21:(-3)+5*(-9)
21:(-3)=-7
5*(-9)=-45
49-(-7)=-56
-45+(-56)=11
-37+(-80-8*(-6)):8
8*(-6)=-48
-80-(-48)=-128
-128:8=16
-37+16=53
10*(-8)+(48-83):(-5)
48-83=-35
10*(-8)=-80
-35:(-5)=-7
-80+(-7)=-73
(9*(-2)-79+17):(-10)
9*(-2)=-18
-18-79=-61
-61+17=-44
-44:(-10)=-4.4