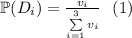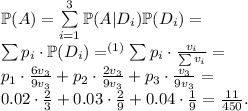- событие "вытащена деталь под номером i".
- событие "вытащена деталь под номером i".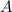 - событие "вытащенная деталь бракована".
- событие "вытащенная деталь бракована".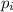 - соответствующие вероятности брака.
- соответствующие вероятности брака.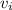 - производительности станков.
- производительности станков.

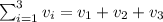 деталей, а вероятности событий
деталей, а вероятности событий  вычисляются как отношения количества подходящих деталей ко всем деталям в ящике, то есть
вычисляются как отношения количества подходящих деталей ко всем деталям в ящике, то есть