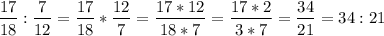
Как доказать тождество?
Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».
В случаях, когда тождество не содержит переменных и иррациональности, можно вычислить правую и левую части.
Пример. Доказать тождество
(
2
,
5
+
5
⋅
6
15
)
2
=
22
−
1
,
75
.
(
2
,
5
+
5
⋅
6
15
)
2
=
22
−
1
,
75
(
2
,
5
+
6
3
)
2
=
20
,
25
(
2
,
5
+
2
)
2
=
20
,
25
(
4
,
5
)
2
=
20
,
25
20
,
25
=
20
,
25
Тождество доказано.
В более сложных случаях, доказывая тождество, приходится прибегать к преобразованиям, потому что посчитать «в лоб» уже нельзя. При этом можно:
Преобразовывать обе части одновременно (как в примере выше).
Преобразовывать только левую или только правую часть.
Переносить слагаемые через равно, меняя знак.
Умножать левую и правую часть на одно и то же число.
Использовать все математические правила и формулы (формулы сокращенного умножения, свойства степени, правила работы с дробями и разложения на множители и так далее и тому подобное). Именно пятый пункт при доказательстве тождеств используется чаще всего, поэтому все эти свойства и правила нужно знать, помнить и уметь использовать.
Пример. Доказать тождество
(
a
+
b
)
2
+
(
a
−
b
)
2
=
2
(
a
2
+
b
2
)
.
(
a
+
b
)
2
+
(
a
−
b
)
2
=
2
(
a
2
+
b
2
)
Работаем с левой частью, не трогая правую.
С формул сокращенного умножения раскроем скобки слева,…
a
2
+
2
a
b
+
b
2
+
a
2
−
2
a
b
+
b
2
=
2
(
a
2
+
b
2
)
…затем приводим подобные слагаемые,…
2
a
2
+
2
b
2
=
2
(
a
2
+
b
2
)
…после чего вынесем за скобку двойку.
2
(
a
2
+
b
2
)
=
2
(
a
2
+
b
2
)
Обе части равны - тождество доказано
Пример. Доказать тождество
x
2
+
1
x
2
=
(
x
+
1
x
)
2
−
2
.
x
2
+
1
x
2
=
(
x
+
1
x
)
2
−
2
Преобразуем правую часть, не трогая левую.
Раскроем скобки с формулы квадрата суммы,…
x
2
+
1
x
2
=
x
2
+
2
x
⋅
1
x
+
1
x
2
−
2
…у одно из слагаемых, сократив
x
и
1
x
, …
x
2
+
1
x
2
=
x
2
+
2
+
1
x
2
−
2
… и приводим подобные слагаемые (
2
и
−
2
).
x
2
+
1
x
2
=
x
2
+
1
x
2
Слева и справа одинаковые выражения, значит тождество доказано.
ВОТ ТЕ ПОДСКАЗКА КАК ДЕЛАТЬ)))
4000 м
Пошаговое объяснение:
1)1400 м :35% =40 м
2)40*100=4000 м