Исследовательская работа
Внутренняя точка равностороннего треугольника
2-я часть. Доказательство гипотезы
Описание ситуации
В равностороннем треугольнике произвольно отмечаем внутреннюю точку и проводим расстояния от этой точки до сторон треугольника.
Исследуемая проблема
Величина суммы расстояний.
Гипотеза
В любом равностороннем треугольнике сумма расстояний от произвольно выбранной внутренней точки до сторон треугольника равна высоте треугольника.
Доказательство гипотезы
1. Нарисуй на листе равносторонний треугольник.
2. Отложи внутри треугольника точку, соедини её с вершинами треугольника.
Этим данный треугольник разделён на (напиши числом) ... треугольника.
3. Проведи расстояния от точки до сторон треугольника.
В каждом из новых треугольников это расстояние — (слово начинается на букву «в») ...
4. Напиши формулу площади для всех трёх полученных треугольников.
Беря во внимание имеющиеся на чертеже элементы, какую формулу площади используем?
a23–√4
a⋅ha2
a⋅b⋅sinγ2
p(p−a)(p−b)(p−c)−−−−−−−−−−−−−−−−−√
5. Сложи площади трёх треугольников, вынеси за скобки общий множитель.
За скобки можно вынести число, которое обозначает
сторону треугольника
высоту
6. Напиши формулу площади данного треугольника.
Закончи доказательство самостоятельно, сравни свои выводы с гипотезой.
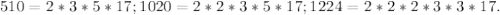
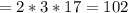(максимальная возможная вместимость вагона)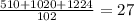
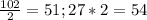(остальные варианты(3,17) не подходят из-за ограничения кол-ва вагонов < 60 )
Обозначим за
Тогда полный износ для изначально передних покрышке составит:
Полный износ для изначально задних покрышке составит:
Получаем систему уравнений:
Вычитая из верхнего уравнения нижнее, получаем:
К чему можно было бы прийти и чисто умозрительно, понимая, что все покрышки должны сделать одинаковый пробег, как на переднем, так и на заднем мосте.
Тогда:
Все величины были вычислены в тысячах километров.
О т в е т :
Чтобы "Lada Vesta" максимально возможное расстояние на указанных покрышках, их нужно поменять местами через
Максимально возможное расстояние на указанных покрышках составит