Пошаговое объяснение:
( sin(x) + cos(x))^2 = 1-sin(x) * cos(x)
разложим уравнение используя (a+b)^ = a^2-ab+b^2
sin(x)^2+2sin(x)cos(x)+cos(x)^2 = 1-sin x * cos x
упрощаем выражение, используя sin(t)^2+cos(t)^2=1
1+2sin(x)cos(x) = 1-sin(x)cos(x)
упрощаем выражение, используя 2sin(t)cos(t)=sin(2t)
1+sin(2x) = 1-sin(x)cos(x)
сократим равные члены в обеих частях уравнения
sin(2x) = -sin(x)cos(x)
переместив выражение в левую часть, прибавляем противоположное ему выражение к обеим частям
sin(2x)+sin(x)cos(x) = -sin(x)cos(x)+sin(x)cos(x)
сумма двух противоположных чисел равна 0
sin(2x)+sin(x)cos(x) = 0
используем sin(2t) = 2sin(t)cos(t)
2sin(x)cos(x)+sin(x)cos(x) = 0
приводим подобные члены
3sin(x)cos(x) = 0
делим обе стороны на 3
sin(x)cos(x) = 0
если произведение равно 0, то как минимум один из множителей равен 0
sin(x) = 0
cos(x) = 0
решаем уравнение относительно х
x = kπ, k∈Z
x =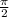 
+kπ, k∈Z
Объединяем
x =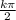 
, k∈Z
6sin²(x) - 5cos(x) - 5 = 0
6 • (1 - cos²(x)) - 5cos(x) - 5 = 0
6 - 6cos²(x) - 5cos(x) - 5 = 0
-6cos²(x) - 5cos(x) + 1 = 0
• Пусть cos(x) = t, тогда cos²(x) = t², причём: | t | ≤ 1
-6t² - 5t + 1 = 0 / • (-1)
6t² + 5t - 1 = 0
(a = 6, b = 5, c = -1)
D = b² - 4ac
D = 5² - 4 • 6 • (-1) = 25 + 24 = 49 = 7²
t₁,₂ = (-b ± √D)/2a
t₁ = (-5 + 7)/2 • 6 = 2/12 = ⅙
t₂ = (-5 - 7)/2 • 6 = -12/12 = -1
• Оба значения подходят под наше условие: | t | ≤ 1, поэтому получаем систему:
[ cos(x) = ⅙
[ cos(x) = -1
[ x₁ = ± arccos(⅙) + 2πn, n ∈ ℤ
[ x₂ = π + 2πn, n ∈ ℤ
x₁ = ± arccos(⅙) + 2πn, n ∈ ℤ
x₂ = π + 2πn, n ∈ ℤ
