С начала XIX в. в сельском хозяйстве Крыма начался процесс специализации. Районы полуострова специализируются в той или иной отрасли, на том или другом виде продукции.
Большой спрос на шерсть на внутреннем и мировом рынках обусловил развитие в степной части полуострова крупных овцеводческих хозяйств промышленного типа. Этому совсем незначительная плотность населения степной части.н. Он активно приглашает в Крым из разных стран специалистов по этой культуре, выписывает лучшие сорта виноградных лоз и всячески поощряет помещиков и предпринимателей, занимавшихся развитием виноградарства. Успешному развитию виноградарства и виноделия в Крыму открытие в 1804 г. в Судаке казенного училища виноделия и виноградарства, основание в 1812 г. магарачского училища виноделия. Об успешном развитии виноградарства в Крыму в первой половине XIX в. свидетельствуют следующие данные:
в конце 20-х годов – около 5800000 кустов;
в конце 30-х – около 12000000 кустов;
в конце 40-х – около 35000000 кустов.
В целом надо отдать должное русскому правительству – оно оценило выгодные условия Крыма и вело дальновидную политику.
Льготные условия предоставлялись не только лицам, занимавшимся виноградарством и овцеводством, но также и тем, кто занимался садоводством. В частности, 7 июля 1803 г. был издан специальный правительственный указ о льготах для лиц, занимавшихся разведением садов. Подобные указы издавались в 1828 и 1830 гг. Лицам, занимавшимся садоводством и виноградарством, отдавались казенные земли в бесплатное пользование и даже в личное «потомственное» владение. В 1830 г. губернатором Новороссии Воронцовым было роздано около 200 десятин земли на Южном берегу в бесплатное пользование частным лицам, которые дали обязательство заниматься на этих участках садоводством. Основными садоводческими районами были долины: Салгирская, Качинская, Альминская, Бельбекская, Булганакская. Площадь, занимаемая фруктовыми садами, постоянно увеличивалась. В пригородных районах успешно развивалось огородничество товарного типа. Так, в районе Евпатории в первой половине XIX в. на больших площадях выращивали лук, который продавали не только в Крыму, но и вывозили в Одессу и даже Константинополь. В первой половине XIX в. в Крыму начинает развиваться табаководство. В предвоенные годы площадь табачных плантаций составляла 336 десятин. Огородничеством и табаководством занимались преимущественно арендаторы. Особенности развития сельского хозяйства Крыма, особенно его специализация, приводили к быстрому развитию внутренней и внешней торговли, к развитию товарно-денежных отношений. Достаточно узко специализированные хозяйства не могли существовать без рынка, они имели ярко выраженный товарный характер. Продукция этих хозяйств – виноград, яблоки и другие фрукты, овощи, табак, шерсть – полностью предназначалась для продажи. В то же время эти хозяйства нуждались в той продукции, которую сами не производили. Развитию товарно-денежных отношений и то обстоятельство, что в сельском хозяйстве края широко использовался наемный труд. Все эти особенности приводили к тому, что сельское хозяйство Крыма становилось на капиталистический путь развития, значительно опережая в этом центральные губернии России.
ДУМАЕМ (ответ Замятина)
Мысль 1. Центр окружности на пересечении перпендикуляров из середин сторон.
Мысль 2 - Середина стороны по формуле D= (A+B)/2
Мысль 3. Коэффициент перпендикуляра: k1 = - 1/k
Мысль 4. Радиус окружности - расстояние от вершины до центра окружности.
Мысль 5. Уравнение окружности со смещенным центром:
(x + a)² + (y + b)² = R²
Пора переходить и к ....
РЕШЕНИЕ.
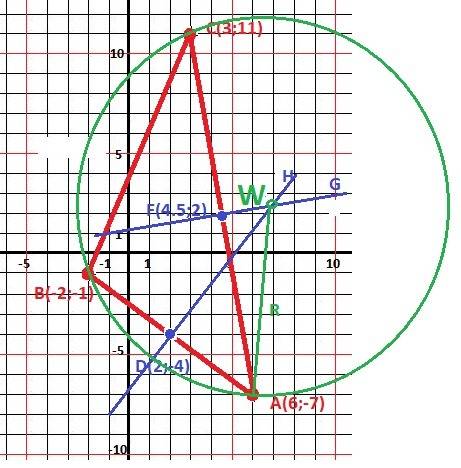
Рисунок к задаче в приложении. Строим треугольник по заданным координатам.
1) Находим середины сторон треугольника.
Dx = (Ax + Bx)/2 = 2, Dy = (Ay+By)/2 = -4 и D(2;-4)
F(4.5;2)
2) Находим уравнения сторон АВ и АС.
k = ΔY/ΔX = (Аy-By)/(Аx-Bx)=(-7--1)/(6--2)=-0,75 - наклон прямой b=Аy-k*Аx=-7-(-0,75)*6=-2,5- сдвиг по оси ОУ
Уравнение АВ: Y=-0,75*x+-2,5
k = ΔY/ΔX = (Аy-Сy)/(Аx-Сx)=(-7-11)/(6-3)=-6 - наклон прямой
b=Аy-k*Аx=-7-(-6)*6=29- сдвиг по оси ОУ
Уравнение АС: Y=-6*x+29
3) Находим уравнения перпендикуляров к прямым АВ и АС.
Уравнение перпендикуляра DH.
k(DH) = - 1/k(AB) = -1/(-0.75) = 4/3 - наклон.
b = Dy - k*Dx - -4 - 4/3*2 = - 6 2/3 - сдвиг
Уравнение DH: Y= 4/3*x - 20/3 или в параметрической форме записи
4*x - 3*y = 20 - уравнение DH - (запомнили - уравнение 1)
Уравнение перпендикуляра FG.
k = 1/6
b = Fy-k*Fx = 2 - 1/6*4.5 = 1.25.
Уравнение FG: Y= x/6 + 5/4 или в параметрической форме:
Y = (2*x+ 15)/12 -> 2*x - 12*y = - 15 -(уравнение 2)
4) Находим точку пересечения перпендикуляров - W (вау) - центр окружности. Решение систему из двух уравнений прямых DH FG.
1) 4*x - 3*y = 20
2) 2*x - 12*y = -15
Получилось решение: Х = 6 11/14 (≈6.8) и У = 2 8/21 (≈2.4)( такое решение).
5) Находим радиус окружности - расстояние между точками А и W по теореме Пифагора.
R²= (Wy-Ay)²+ (Wx-Ax)² = (2 8/21 - (-7))² + (11/14)² ≈ 88.6
6) Уравнение окружности
(х - 6,8)² + (y + 2.4)² = 88.6 - ОТВЕТ
Задача решена, хотя .................. это ответ Замятина - возможны и опечатки, но, главное, АЛГОРИТМ РЕШЕНИЯ..
(2x-4)(x+2)=10
2х²+4х-4х-8=10
2х²=18
х²=9
х1=3. х2= -3
ответ: 3; -3
(2x-1)(x+8)-(x-1)(x+1)= - 7
2х²+16х-х-8-х²+1= -7
х²+15х=0
х(х+15)=0
х=0. х+15=0
х= -15
ответ: 0; -15