1
Пошаговое объяснение:

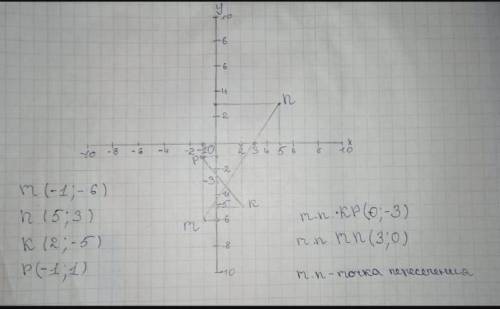
Для начала начертите линию длиной 10 см, и посередине(на 5 см) поставьте точку, также сделайте и вертикальным образом
На верхушке оси ординат(вертикальная полоса) напишите "у", в правом конце абцисс(горинтальная) букву "х". В середине(где стоит точка) букву "О"
Прономеруйте отрезки как показано на фото(номеруйте только четные числа, каждые 2 клетки)
Теперь находим координаты: Первое число координаты - ось абцисс, второе число - ось ординат. Вычислите все координаты, поставив на них точку и написав букву этой координаты.
Соединяем эти точки (буквы) с линейки, как сказано в условии.
Эти соедененные точки однозначно проходят через какую либо ось, и там, где они соприкасаются ставьте точку
Дело за малым: Ниже просто напишите это:
М (-1; -6)
N (5; 3)
К (2; -5)
Р (-1; 1)
И рядом во втором столбике:
т.п. КР (0; -3)
т.п. MN (3; 0)
ответ:
пошаговое объяснение:
x^2+3x+2< =0
(x+1)(x+2)< =0
x € [-2; -1]
нам надо, чтобы этот отрезок попал целиком внутрь промежутка - решения 2 неравенства.
x^2 + 2(2a+1)x + (4a^2-3) < 0
d/4 = (2a+1)^2 - (4a^2-3) = 4a^2+4a+1-4a^2+3 = 4a+4
если это неравенство имеет два корня, то d/4 > 0
a > -1
x1 = -2a-1-√(4a+4) < -2
x2 = -2a-1+√(4a+4) > -1
тогда решение 1 неравенства [-2; -1] целиком находится внутри решения 2 неравенства [x1; x2].
{ -√(4a+4) = -2√(a+1) < = 2a-1
{ √(4a+4) = 2√(a+1) > = 2a
из 1 неравенства
2√(a+1) > = 1-2a
4(a+1) > = 1-4a+4a^2
4a^2-8a-3 < = 0
d/4 = 4^2+4*3=16+12=28=(2√7)^2
a1=(4-2√7)/4=1-√7/2 ~ -0,323
a2=(4+2√7)/4=1+√7/2 ~ 2,323
a € [1-√7/2; 1+√7/2]
из 2 неравенства
а+1 > = a^2
a^2-a-1 < = 0
d=1+4=5
a1 = (1-√5)/2 ~ -0,618
a2 = (1+√5)/2 ~ 1,618
a € [(1-√5)/2; (1+√5)/2]
ответ: a € [1-√7/2; (1+√5)/2]
Пошаговое объяснение:
7/21 = 1/3