Сразу сделаю оговорку- будем считать, что количество монет в каждом мешке одинаково, независимо от того, это мешок с настоящими или с фальшивыми монетами(этого в задании не сказано).
Возможно в моих рассуждениях есть ошибка, но тем не менее, выскажусь:
1) будем считать за одно взвешивание, то действие, когда какое-то количество мешков с монетами положены на весы и ещё не сняты, а к ним продолжают подкладывать другие мешки- если один мешок на левую чашку, то и один мешок на правую.
2) одинаковые мешки(настоящие)-имеют один вес, поэтому, если вначале на левую чашку, а затем на правую будут попадать мешки одинакового веса, то стрелка весов будет находиться по середине (на 0), показывая тем самым равновесие.
3) Но, в тот момент, когда на одну чашку ляжет мешок с настоящими монетами, а на другую с фальшивыми монетами- чашка весов с фальшивым мешком опустится вниз(по условию задания фальшивый мешок тяжелее)
УДАЧИ!
Пошаговое объяснение:
2
Пошаговое объяснение:
У нас 2 окружости:
g: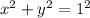
v: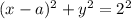
Окружность g находится в начале координат и имеет радиус 1.
Окружность v имеет радиус 2 находится на 0 по y и может перемещаться по x через изменение параметра a.
Центры обоих окружностей лежат на прямой OX. Значит существует 2 точки их касания.
Эти параметры даже можно додумать аналитически. Такие значения а, при которых расстояние между двумя центрами равно сумме радиусов.
R(v) = 2, R(g)=1. SR = R(v) + R(g) = 3.
a = ± 3.