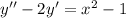 Дифференциальное уравнение является дифференциальным уравнением второго порядка со специальной право частью.
Дифференциальное уравнение является дифференциальным уравнением второго порядка со специальной право частью.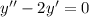 переходя к характеристическому уравнению
переходя к характеристическому уравнению 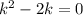 имеем,
имеем, 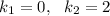
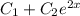 - общее решение однородного уравнения.
- общее решение однородного уравнения.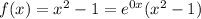
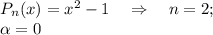
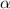 с корнями характеристического уравнения и, принимая во внимания, что
с корнями характеристического уравнения и, принимая во внимания, что 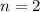 частное решение будем искать в виде: yч.н. =
частное решение будем искать в виде: yч.н. = 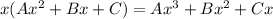
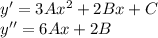 и подставляем в исходное уравнение
и подставляем в исходное уравнение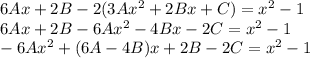
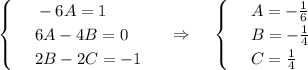
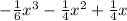 - частное решение.
- частное решение.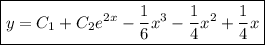
6 (км/час) - скорость течения реки.
Пошаговое объяснение:
Рухаючись проти течії річки теплохід за 3 год пройшов відстань у 69км. Знайди швидкість течії річки якщо власна швидкість теплохода 29км/час.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость течения реки.
29-х - скорость теплохода против течения реки.
По условию задачи уравнение:
(29-х) *3=69
87-3х=69
-3х=69-87
-3х= -18
х= -18/-3
х=6 (км/час) - скорость течения реки.
Проверка:
(29-6)*3=23*3=69 (км), верно.