Question

Зная что 3/4 от а равна 5/6 от в и 1/2 от с сравните а, в, а если а, в, с больше 0
Можно вы решите без системы мы её ещё не проходили ​

Answer 1

ответ: b < a < c

Пошаговое объяснение:

1.

$\frac{3}{4} a=\frac{5}{6} b$

Рассмотрим это равенство. Домножим левую дробь на 6, правую - на 4, чтобы прийти к общему знаменателю:

$\frac{3\cdot 6}{4\cdot 6} a=\frac{5 \cdot 4}{6 \cdot 4} b\\\\\frac{18}{24} a=\frac{20}{24} b \, \bigg| \cdot 24\\\\18a=20b \, \bigg| :18\\\\a=\frac{20}{18} b$

Получим равенство (1), откуда следует, что b < a.

2.

$\frac{3}{4} a=\frac{1}{2} c$

Рассмотрим это равенство. Домножим правую дробь на 2, чтобы прийти к общему знаменателю:

$\frac{3}{4} a=\frac{1\cdot 2}{2\cdot 2} c\\\\\frac{3}{4} a=\frac{2}{4} c \, \bigg| \cdot 4\\\\3a=2c \, \bigg| :3\\\\a=\frac{2}{3} c$

Получим равенство (2), откуда следует, что a < c.

3. Теперь сравним c и b. Из равенства (2) возьмем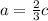  $a=\frac{2}{3} c$ и подставим в равенство (1):

$a=\frac{20}{18} b$  

$a=\frac{2}{3} c =\frac{20}{18} b$

Домножим дробь при c на 6, чтобы прийти к общему знаменателю:

$\frac{2\cdot 6}{3\cdot 6} c =\frac{20}{18} b\\\\\frac{12}{18} c =\frac{20}{18} b \, \bigg| \cdot 18\\\\12c=20b \, \bigg| :12 \\\\c=\frac{20}{12} b$

Откуда следует, что b < c.

Итак, мы получили следующее:

b < a

a < c

b < c

Откуда следует, что b < a < c.