Найдем начала общее решение соответствующего однородного дифференциального уравнения
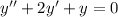 (*)
(*)
Воспользовавшись заменой Эйлера 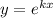 , мы получим характеристическое уравнение
, мы получим характеристическое уравнение
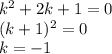
Общее решение уравнения (*)
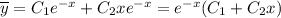
Далее нужно найти частное решение. Рассмотрим функцию:
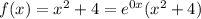
Здесь 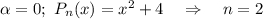
Сравнивая 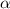 с корнями характеристического уравнения и, принимая во внимая, что
с корнями характеристического уравнения и, принимая во внимая, что 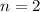 частное решение будем искать в виде
частное решение будем искать в виде
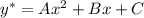
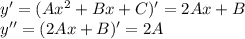
Подставляем все это в исходное дифференциальное уравнение
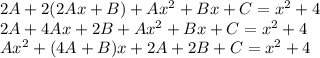
Приравниваем коэффициенты при степени x
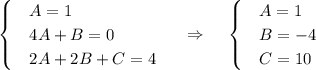
Частное решение: 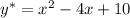
Общее решение линейного неоднородного дифференциального уравнения:
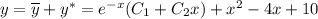
P AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SPAM
SAM
AM
AMP
AMSP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AMSP
ASP
SP
SPM
SPAM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SP AM
SPAM
SAM
AM
AMP
AMSP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AM SP
AMSP
ASP
SP
SPM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
SPAM
Must Waste More Time...