На доске было написано 30 натуральных чисел (необязательно различных), каждое из которых не
превосходит 40. Среднее арифметическое написанных чисел равнялось 1. Вместо каждого из чисел
на доске написали число, в два раза меньшее первоначального. Числа, которые после этого
оказались меньше 1, с доски стёрли.
а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше 14?
ответ: Ода Онет
6) могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 12, но меньше 13?
ответ: Ода Онет
в) Найди наибольшее возможное значение среднего арифметического чисел, которые остались на
доске
, где n - количество букв в алфавите. Значит, для n=7 получим:
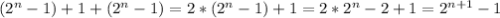
Такие соображения можно продолжить и дальше. Например, 5 уравнений с 8-ю неизвестными имеют бесконечно много решений, причем произвольные значения можно давать трем неизвестным и т. п.
Решать системы уравнений с большим числом неизвестных приходится редко. Следует при этом решении пользоваться по возможности всеми особенностями уравнений, чтобы упростить решение.
Рассмотрим 2 примера. Пример 1:
x + y + 2z – t = 9
x + y – 2z + t = 7
x – y + z + 2t = –9
x – y – z – 2t = 5
Сложив 1-е и 2-е уравнения по частям, мы получим очень простое уравнение только с двумя неизвестными, а именно
2x + 2y = 16 или x + y = 8.
Сложив по частям 3-е и 4-е уравнения, получим:
2x – 2y = –4 или x – y = –2.
Теперь легко решить 2 полученных уравнения (x + y = 8 и x – y = –2), и тогда найдем x = 3 и y = 5.
Подставляя эти значения в 1-е и в 3-е уравнения, получим:
3 + 5 + 2z – t = 9 или 2z – t = 1
3 – 5 + z + 2t = –9 или z + 2t = –7
Подстановка этих значений во 2-е и 4-е уравнения приведет к таким же точно уравнениям.
Теперь остается решить 2 уравнения с 2 неизвестными: