а) 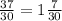
б) 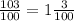
в) 
Пошаговое объяснение:
Привет! Давай решать.
А)
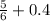
Переводим десятичную в обычную.
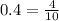
Получается такой пример:
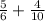
Сейчас, нужно найти общий знаменатель:
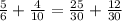
В первой дроби знаменатель и числитель умножили на 5, во второй на 3.
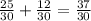
Превращаем в целую, несократимую дробь.
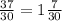
Вот первая дробь решена.
Б)
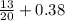
Десятичную превращаем в обычную.

Приводим дроби к общему знаменателю:
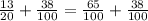
В первой дроби знаменатель и числить умножаем на 5, а во второй ничего не умножаем. Вычисляем:
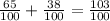
Превращаем в целую, несократимую дробь:
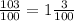
Вот вторая дробь решена.
В) Уравнение.
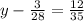
Приводим дроби к общему знаменателю:
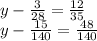
Переносим дробь с левой части в правую через равно, меняя знак:
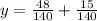
Вычисляем:
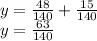
Вот уравнение и решено!
Теперь приравняем производную к нолю и решим полученное уравнение
6x(x-1)=0
6х=0 х-1=0
х=0 х=1
Нанесем полученные точки на ось Ох и определим знак функции.
ОБЯЗАТЕЛЬНО НАРИСОВАТЬ. таким образом получим три промежутка
1. (-беск; 0): у(-2)=6*(-2)(-2-1)=-12*(-3)=36, >0
2. [0;1]: y(0,5)=6*0,5*(0,5-1)=3*(-0,5)-1,5 <0
3.(1;беск): y(2) 6*2(2-1)=12*(1)=12, >0
И так видим что при прохождении точек х=0 и х=1 функции меняет свой знак следовательно эти точки и являются экстремумами функции
ответ:х=0 и х=1