45-5=на 40 коробок больше привезли в магазин вечером.
40:4=10 тортов в одной коробке.
10×5=50 тортов привезли утром.
10×45=450 коробок привезли вечером.
50+450=500 тортов всего привезли в магазин.
Верные утверждения:
1) Теорема: параллелограмм является прямоугольником, если: а) его диагонали равны; б) серединный перпендикуляр к какой-либо стороне параллелограмма является его осью симметрии.
2) Квадрат - это прямоугольник, у которого все стороны являются равными.
6) Сумма внутренних углов параллелограмма = 360°.
7) Они могут быть равны, если это ромб. Но во всех остальных случаях это так.
10) Жесткая фигура — это фигура, не подверженная деформации.
Неверные утверждения:
3) Квадрат, прямоугольник и ромб - это частные случаи параллелограмма. Не все и не всегда.
4) Квадрат, прямоугольник и ромб - это частные случаи параллелограмма. Значит, такое возможно.
5) Квадрат обладает всеми свойствами ромба, параллелограмма и прямоугольника. Квадрат - это всегда параллелограмм.
8) Теорема: диагонали параллелограмма делятся точкой пересечения пополам.
9) Такое возможно не всегда, а только в одном случае, когда параллелограмм - ромб.
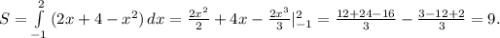
Советую нарисовать задачу в виде схемы,если для объяснения ребёнку)
Пошаговое объяснение: