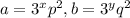, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
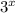, получим уравнение 
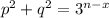. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 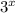, имеем 
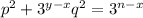. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
а) Что бы найти скорость, нужно расстояние разделить на время, т.е. 90км/ч делишь на время - 1.5ч и получается 60км/ч. А от В до развилки 75 км(165 - 90), анологично, 75 делишь на 1.5 и получается 50 км/ч.
б) Сначала нужно найти время за которое теплоход доплыл в город А, 63км делишь на 36км/ч(т.к. теплоход движется по течению реки, а скорость течения 4км/ч, 32+4) и получается 1.75 часа, дальше находим время, за которое он проплыл обратно, 63 делим на 28(отнимаем 4км/ч, т.к. против течения)получается 2.25часа, ну а дальши от 2.25 отнимай 1.75 и получается 0.5. Т.е. теплоходу потребуется на пол часа больше времени, что бы доплыть обратно.