Пусть второй рабочий делает х деталей в час, тогда первый рабочий делает ( х+3) детали в час
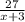 часов тратит первый рабочий на изготовление 27 деталей
часов тратит первый рабочий на изготовление 27 деталей
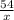 часов тратит второй рабочий на изготовление 54 деталей.
часов тратит второй рабочий на изготовление 54 деталей.
По условию сказано, что время первого на 6 часов меньше.
Составляем уравнение
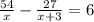
х≠0 х+3≠0
54(х+3)-27·х=6х(х+3)
54х+162-27х=6х²+18х
6х²-9х-162=0
2х²-3х-54=0
D=(-3)²-4·2·(-54)=9+432=441=21²
x=(3-21)/4 <0 или х=(3+21)/4=6 деталей в час изготавливает второй
54:6=9 часов работает второй
Проверка
тогда первый в час делает (6+3)=9 деталей
и
27:9=3 часа работает первый
разница во времени
9-3=6 часов - верно
ответ. 6 деталей в час изготавливает второй рабочий.
1) Найти области определения и значений данной функции f.
Для аргумента и функции нет ограничений: их значения - вся числовая ось.
2) Выяснить, обладает ли функция особенностями, облегчающими исследование, т. е. является ли функция f: а) четной или нечетной:
f(-x)=(-x)³−1 = -x³−1 = -(x³+1). Значит, функция не чётная и не нечётная.
б) не периодическая.
3) Вычислить координаты точек пересечения графика с осями координат:
- пересечение с осью Оу (х = 0), у = -1.
- пересечение с осью Ох (у = 0), x³−1 = 0, x³ = 1, x = ∛1 = 1.
4) Найти промежутки знакопостоянства функции f.
На основе нулей функции имеем:
- функция отрицательна при х < 1 (x ∈ (-∞; 1),
- функция положительна при х > 1 (x ∈ (1; +∞).
5) на каких промежутках функция f возрастает, а на каких убывает.
Найти точки экстремума, вид экстремума (максимум или минимум) и вычислить значения f в этих точка.
Находим производную функции и приравниваем нулю.
y' = 3x² = 0, x = 0 это критическая точка. Находим знаки производной левее и правее этой точки. Так как переменная в квадрате, то знак её положителен. Значит, функция на всей области определения возрастает.
Поэтому не имеет ни минимума, ни максимума.
6) Вторая производная y'' = 6x. Поэтому в точке х = 0 функция имеет перегиб. При x < 0 график функции выпуклый, при x > 0 вогнутый.
7) Асимптот функция не имеет.

а какое 1 задача мне не видно
Пошаговое объяснение: