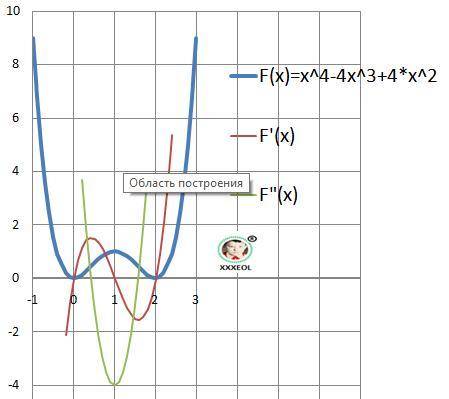
ДАНО: Y(x) = x⁴ - 4*x³+ 4*x² .
ИССЛЕДОВАНИЕ:
Описание ГЛАЗАМИ: Функция четвертого порядка с положительным коэффициентом - примерно парабола и ветви вверх. Должно быть четыре корня.
1. Область определения. Непрерывная. Разрывов нет.
D(x) = (-∞;+∞)
2. Нули функции - пересечение с осью ОХ.
Y= x²*(4*x²- 4*x +4) = 0
х₁ =0 и х₃ = 2 Двух других нет.
Пересечение с осью ОУ - Y(0) = 0/
3. Интервалы знакопостоянства/
Положительна: Y>0 X∈(-∞;0)∪(0;2)∪(2;+∞)
Y=0 X=(0;2) - в нулях функции. корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 4*x³ -12*x² + 8x = 4*x*(x²- 12*x + 2) = 0
Точки экстремумов: x = 1, x = 2, x = 0
5 Локальные экстремумы:
Ymin(0) = Y(2) = 0, Ymax(1) = 1.
6. Интервалы монотонности.
Убывает: Х∈(-∞;0) ∪ (1;2)
Возрастает: Х∈(0;1) ∪ (2;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 12*x² -24х +8 = 0
x₈ ≈ 0.42 и х₉ = 1.58 - точки перегиба.
8. Вогнутая - "ложка" - Х∈(-∞;0,42)∪(1.58;+∞) - вне корней.
Выпуклая - "горка" - Х∈(х₈=-0,42;1.58)
График на рисунке в приложении.
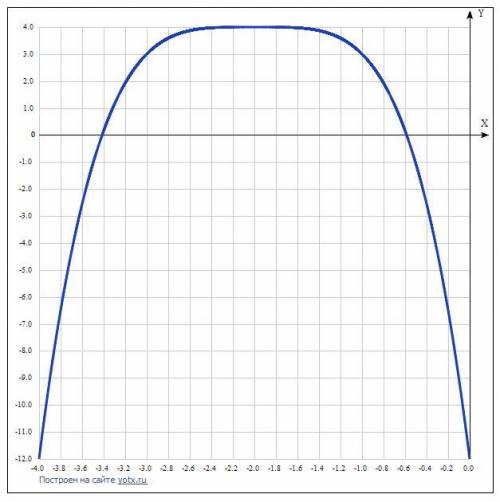
Дана функция y=4-(x+2)⁴.
Переменная в чётной степени, поэтому график функции похож на параболу.
Так как перед переменной стоит знак минус, то ветви графика направлены вниз.
Функция имеет максимум при х = -2, тогда у = 4.
Точки пересечения с осью Ох аналитически определить очень сложно, так как надо решить уравнение 4 степени.
С вс программ эти точки найдены.
х1 = -2 - √2, х2 = 2 - √2.
Пересечение с осью Оу находится легко - подстановкой х = 0 в уравнение: у = 4 - 2^4 = 4 - 16 = -12.
Для построения графика даются координаты точек:
y(x)=4−(x+2)^4
x y
-4.0 -12
-3.8 -6.5
-3.6 -2.55
-3.4 0.16
-3.2 1.93
-3.0 3
-2.8 3.59
-2.6 3.87
-2.4 3.97
-2.2 4
-2.0 4
-1.8 4
-1.6 3.97
-1.4 3.87
-1.2 3.59
-1.0 3
-0.8 1.93
-0.6 0.16
-0.4 -2.55
-0.2 -6.5
0.0 -12.
В пределах от х = -2,2 до х = -1,8 значения округлены, они не точно равны 4, кроме х = -2.
Хочу балов 674р87о748о4584о7о6878о6
Пошаговое объяснение:
143525ваыпин54цни54иц7гн37335678