2·π·p² кв. единица
Пошаговое объяснение:
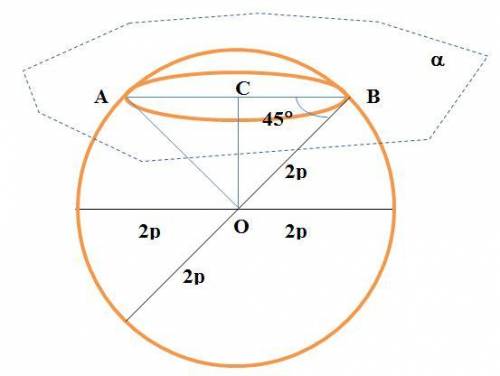
Пусть через конец диаметра проведена плоскость α под углом ∠OBC=45º (также ∠OAC=45º, см. рисунок). Диаметр шара равен 4·p, откуда следует, что радиус шара OB =2·p (также OA =2·p).
При пересечении шара и плоскости α образуется круг радиуса CВ. Тогда площадь этого круга равна S=π·CB².
Определим радиус CB следующим образом. Так как ∠OBC=∠OAC=45º, то треугольник ABO, образованный из радиусов шара OB, OA и диаметром круга, прямоугольный с прямым углом ∠AOB:
∠AOB=180° - ∠OBC - ∠OAC = 180° - 45° - 45° = 90°.
Поэтому, по теореме Пифагора
AB²=OA²+OB²=(2·p)²+(2·p)²=4·p²+4·p²=8·p².
Но CB²=(AB/2)²=AB²/4=8·p²/4=2·p², и поэтому
S=π·CB²=π·2·p²=2·π·p² кв. единица.
АМ - биссектриса <А, значит <ВАМ=<ДАМ
ДМ - биссектриса <Д, значит <СДМ=<АДМ
Удаленность точки от прямой измеряется длиной перпендикуляра на прямую.
ΔАВМ и ΔСДМ - тупоугольные, значит их высоты, проведенные из острой вершины, попадают не на сторону этого треугольника, а на ее продолжение.
Т.е. высота ΔАВМ, опущенная из вершины М, лежит на продолжении стороны АВ - обозначим высоту МК.
Аналогично высота ΔСДМ, опущенная из вершины М, лежит на продолжении стороны СД - обозначим высоту МР.
Также опустим из точки М высоту ΔАМД - обозначим высоту МН.
Нужно доказать МК=МР=МН.
ΔАВМ=ΔАНМ - прямоугольные треугольники, равные по гипотенузе и острому углу (АМ-общая, <КАМ=<НАМ), значит МК=МН
ΔАКМ=ΔАНМ - прямоугольные треугольники, равные по гипотенузе и острому углу (АМ-общая, <КАМ=<НАМ), значит МК=МН
ΔДРМ=ΔДНМ - прямоугольные треугольники, равные по гипотенузе и острому углу (ДМ-общая, <РДМ=<НДМ), значит МР=МН.
Следовательно, МК=МР=МН.