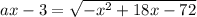
(a² + 1)x² - (6a + 18)x + 81 = 0
D = (6a + 18)² - 4*81(a² + 1) = 36a² + 216a + 324 - 324a²- 324 = -288a² +216a = -a(288a-216)
Квадратичное уравнение имеет единственное решение при условии что дискриминант равен 0
a(288a - 216) = 0
a₁ = 0 Не входит в ОДЗ так как при а=0 ax - 3 = -3<0
a₂ = -216/288 = 0,75 Входит в ОДЗ
ответ: 0,75
Рішення:
ОДЗ рівняння ax-3> 0
Зведемо обидві частини рівняння в квадрат
a²х² + 9 - 6ax = -x² + 18x - 72
(a² + 1) x² - (6a + 18) x + 81 = 0
D = (6a + 18) ² - 4 * 81 (a² + 1) = 36a² + 216a + 324 - 324a²- 324 = -288a² + 216a = -a (288a-216)
Квадратичне рівняння має єдине рішення за умови що дискримінант дорівнює 0
a(288a - 216) = 0
a₁ = 0 Чи не входить в ОДЗ так як при а = 0 ax - 3 = -3 <0
a₂ = -216/288 = 0,75 Входить в ОДЗ
Відповідь: 0,75
f(x)=1/3 x^3-x^4+5
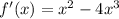
найдём стационарные точки:
х²-4х³ = 0
х²*(4х-1) = 0
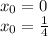
Достаточное условие наличия экстремума в точке - производная меняет знак при переходе. Найдём значения производной на интервалах (возьмём значения: 1(0<0.25<1) , 1/5(0<1/5<1/4) и -1 (-1<0<1/4)
f'(1) = 1² - 4*(1³) = -3
f'( 1/5) = 0,2² - 4*(0,2³) = 0,04 - 4*(0,008) = 0,008 (Знак поменялся, точка 0,25 - точка минимума)
f'(-1) = (-1)²-4*(-1)³ = 1-4*(-1) = 1 + 4 = 5 знак остался прежним, поэтому точка экстремума Одна
ответ: х = 0,25 - точка экстремума
5,3,1
Пошаговое объяснение:
на верхней грани будет единица, на правой-боковой- пятерка, на левой-боковой- тройка.